必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 応用情報技術者
  3. 平成23年度特別問題一覧
  4. 平成23年度特別問題6-解答・解説-分析

平成23年度特別問題

問題6

葉以外の節点はすべて二つの子をもち、根から葉までの深さがすべて等しい木を考える。この木に関する記述のうち、適切なものはどれか。ここで、深さとは根から葉に至るまでの枝の個数を表す。

ア 枝の個数がnならば、葉を含む節点の個数もnである。
イ 木の深さが n ならば，葉の個数は 2n-1 である。
ウ 節点の個数がnならば、深さはlog2nである。
エ 葉の個数がnならば、葉以外の節点の個数はn-1である。

葉以外の節点はすべて二つの子をもち、根から葉までの深さがすべて等しい木を考える。この木に関する記述のうち、適切なものはどれか。ここで、深さとは根から葉に至るまでの枝の個数を表す。

ア 枝の個数がnならば、葉を含む節点の個数もnである。
イ 木の深さが n ならば，葉の個数は 2n-1 である。
ウ 節点の個数がnならば、深さはlog2nである。
エ 葉の個数がnならば、葉以外の節点の個数はn-1である。

解答：エ

＜解説＞

完全二分木（葉以外の節点はすべて二つの子をもち、根から葉までの深さがすべて等しい木）は、次の図のようになる。

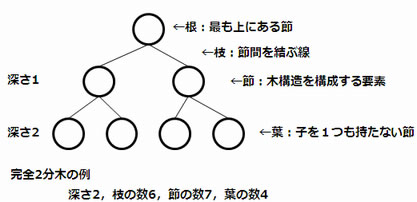
ア × 枝の個数がnならば、葉を含む節点の個数はn+1である。
イ × 木の深さが n ならば，葉の個数は 2n である。
ウ × 節点の個数が n ならば，深さは (log2(n+1))-1 である。
エ ○ 葉の個数がnならば、葉以外の節点の個数はn-1である。