必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 基本情報技術者
  3. 平成22年度春季問題一覧
  4. 平成22年度春季問題2-解答・解説-分析

平成22年度春季問題

問題2

Ｘ 及び Ｙ はそれぞれ0又は1の値をとる変数である。 Ｘ □ Ｙ を Ｘ と Ｙ の論理演算としたとき，次の真理値表が得られた。 Ｘ □ Ｙ の真理値表はどれか。

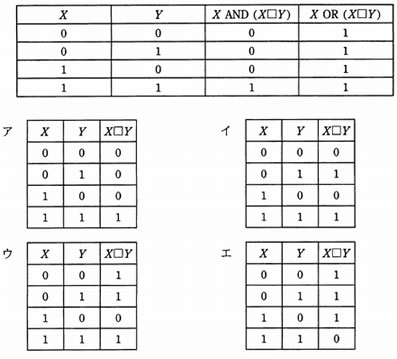
Ｘ 及び Ｙ はそれぞれ0又は1の値をとる変数である。 Ｘ □ Ｙ を Ｘ と Ｙ の論理演算としたとき，次の真理値表が得られた。 Ｘ □ Ｙ の真理値表はどれか。

解答：ウ

＜解説＞

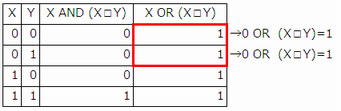
  1. X，Yが0のときX OR （X □Y ）が1、 X が0，Y がともに1のときX OR （X □Y ）が1となるためには，（X □Y ）が1でなくてはならない。
    選択肢の中でこれを満たすのは、ウとエである。
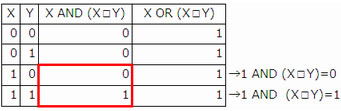
  2. X が1，Y が0のときX AND （X □Y ）が0となるためには，（X □Y ）が1でなくてはならない
    X，Y がともに1のときX AND （X □Y ）が1となるためには，（X □Y ）が1でなくてはならない。
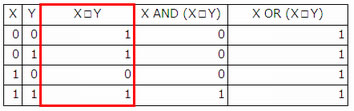
  3. よって真理値表は、次のようになる。