問題1
Xは，0以上65,536未満の整数である。xを16ビットの2進数で表現して上位8ビットと下位8ビットを入れ替える。得られたビット列を2進数とみなしたとき，その値をxを用いた式で表したものはどれか。ここで，a div bはaをbで割った商の整数部分を，a mod bはaをbで割った余りを表す。また，式の中の数値は10進法で表している。
| ア | (x div 256)＋(x mod 256) |
| イ | (x div 256)＋(x mod 256)×256 |
| ウ | (x div 256)×256＋(x mod 256) |
| エ | (x div 256)×256＋(x mod 256)×256 |
解答・解説を見る
解答：イ
シフト演算では、次のように左シフト，右シフトを行う。
- X を n ビット右シフト→X を 2nで割った商
- X を n ビット左シフト→X を 2n倍した積
例として16ビットの2進数 00000000 11111111の上位ビットと下位8ビットを入れ替える。
- Xの上位8ビットを右シフトするには、X を 256(28)で割る。
- Xの下位8ビットは、X を 256(28)で割った余りである。
- 2の結果を8ビット左シフトするには、256(28)倍する。
1～3を整理すると次のようになる。
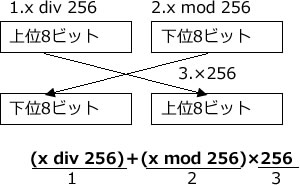
よってイが正解である。