問題79
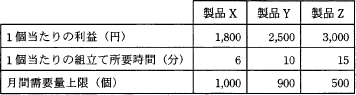
ある工場では表に示す3製品を製造している。実現可能な最大利益は何円か。ここで、各製品の月間需要量には上限があり、組立て工程に使える工場の時間は月間 200 時間までとする。
| ア | 2,625,000 |
| イ | 3,000,000 |
| ウ | 3,150,000 |
| エ | 3,300,000 |
解答・解説を見る
解答：エ
- 時間当たりの利益＝１個当たりの利益÷１個あたりの組立所要時間を求める
製品Ｘ時間当たりの利益 ＝ 1,800÷6 ＝300（円／分) 製品Ｙ時間当たりの利益 ＝ 2,500÷10＝250（円／分) 製品Ｚ時間当たりの利益 ＝ 3,000÷15＝200（円／分)
よって、製品Ｘ、製品Ｙ、製品Ｚの順に利益が高い。 - 製品Ｘを製造した時の利益額と残り時間を計算する。
製品Ｘの利益 ＝ 1,800×1,000＝1,800,000（円） 残り時間 ＝ 12,000－(6×1,000)＝6,000（分） - 次に利益が高い製品Ｙを製造する。製品Ｙの１個当たりの組立て所要時間は、 10 分なので、
製品Yの製造可能個数 ＝ 6,000÷10 製品Yの利益 ＝ 2,500×600＝1,500,000（円） - 製品Ｚを作っている時間はない
- 最大利益を計算する
1,800,000（円）＋1,500,000（円）＝3,300,000（円 ）
よってエが正解である。