問題14
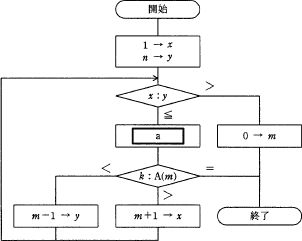
昇順に整列済の配列要素A(1)，A(2)，…，A(n) から，A(m)＝k となる配列要素A(m) の添字 m を2分探索法によって見つける処理を図に示す。終了時点で m＝0 の場合は，A(m)＝k となる要素は存在しない。図中の a に入る式はどれか。ここで，／ は，小数点以下を切り捨てる除算を表す。
| ア | (x + y) → m |
| イ | (x + y)／2 → m |
| ウ | (x - y)／2 → m |
| エ | (y - x)／2 → m |
解答・解説を見る
解答：イ
2分探索法は、整列(ソート)済みのデータ列に対して行う探索方法で、データ列の中央の値を見て、検索したい値との大小関係を用いて、検索したい値が中央の値の右にあるか、左にあるかを判断して、探索範囲を狭めながら行っていく方法である。
[ a ] に入る式は，この中間点を求めて添字 m に代入する式である。
ｍは、中央の値になるので、( x ＋ y ) ／2 → m となる。
よってイが正解である。