問題77
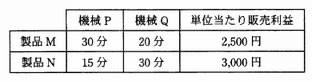
製品 M，N を，機械 P，Q による２工程で生産している。表は，各製品を１単位生産するために要する各機械の所要時間，及び各製品の１単位当たりの販売利益を示す。機械 P，Q の月間稼働可能時間はいずれも 200 時間である。販売利益が最大となるように製品 M，N を生産し，すべてを販売したときの販売利益は何万円か。ここで，製品 M，N ともに生産工程の順番に制約はなく，どちらの機械を先に使用しても製品は生産できるものとする。
| ア | 110 |
| イ | 120 |
| ウ | 135 |
| エ | 140 |
解答・解説を見る
解答：ウ
製品Mをm単位，製品Nをn単位生産し，販売したとする。機械Pの月間稼動可能時間の制約より次の式を満たす必要がある。
m／2＋n／4≦200
2m＋n≦800
機械Qの月間稼動可能時間の制約より，次の式を満たす必要がある。
m／3＋n／2≦200
2m＋3n≦1200
製品M，Nの単位当たりの販売利益がそれぞれ2,500円，3,000円なので，製品Mをm単位，製品Nをn単位生産し，販売した場合の販売利益Rは
R＝2500m＋3000n … ①
販売利益が最大となるのは，以下の直線②，③の交点を式①が通るときである。
2m＋n＝800 … ②
2m＋3n＝1,200 … ③
直線②，③の交点を求めるとｍ＝300，ｎ＝200になる。
よってこのときの販売利益Rは
R＝2,500×300＋3,000×200＝750,000＋600,000＝1,350,000円（135万円）