問題3
探索表の構成法を例とともにa～cに示す。探索の平均計算量が最も小さい探索手法の組合せはどれか。ここで、探索表のコードの空欄は表の空きを示す。
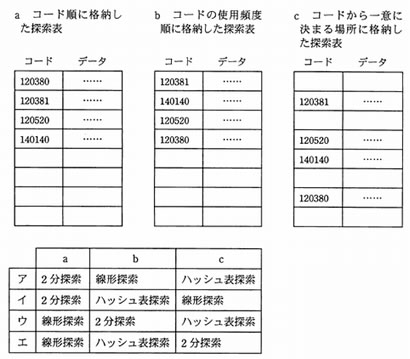
解答・解説を見る
解答：ア
- [a コード順に格納した探索表：2分探索]
- 2分探索は、予めソートされたデータ列を二つに分けて、そのどちらに検索対象が含まれているか判断するという手順を再帰的に繰り返していく検索方法。
⇒aは、 コード順に格納されているので、2分探索法が適している。 - [b コードの使用頻度順に格納した探索表：線形探索]
- 線形探索は、対象データを検索範囲のデータと先頭から順に1つずつ比較し、一致するものを検索する方法。
⇒bは、使用頻度順にならんでいるので先頭から順番に検索すると早く見つけることができるので、線形探索が適している。 - [c コードから一意に決まる場所に格納した探索表：ハッシュ探索]
- ハッシュ探索は、キーの値を基に格納先（記録媒体上）のアドレスを算出し、そのアドレス位置にあるデータを検索する方法。
⇒cは、コードから格納場所を探索するのでハッシュ探索が適している。
したがって、アが正解である。