全体集合S 内に部分集合A とB があるとき、A ∩ B に等しいものはどれか。
ここで、A ∪ B はA とB の和集合、A ∩ B はA とB の積集合、A はS におけるA の補集合、A -B はA からB を除いた差集合を表す。

ア	A -B
イ	(A ∪ B )-(A ∩ B )
ウ	(S -A ) ∪ (S -B )
エ	S -(A ∩ B )

全体集合S 内に部分集合A とB があるとき、A ∩ B に等しいものはどれか。
ここで、A ∪ B はA とB の和集合、A ∩ B はA とB の積集合、A はS におけるA の補集合、A -B はA からB を除いた差集合を表す。

ア	A -B
イ	(A ∪ B )-(A ∩ B )
ウ	(S -A ) ∪ (S -B )
エ	S -(A ∩ B )

解答：ア

＜解説＞

論理式A ∩ B をベン図で表現すると次のようになる。

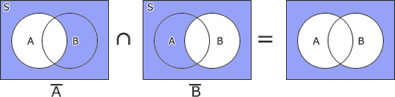
ア～エの論理式をベン図で表すと次の様になる。

ア	○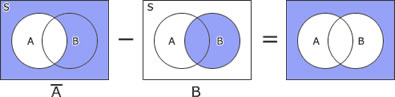
イ	×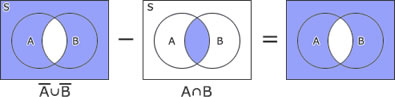
ウ	×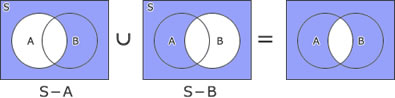
エ	×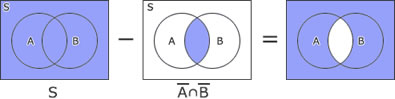

したがって、アが正解である。