必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 応用情報技術者
  3. 平成26年度秋季問題一覧
  4. 平成26年度秋季問題4-解答・解説-分析

平成26年度秋季問題

問題4

配列A[1]、A[2]、…、A[n ]でA[1]を根とし、A[i ]の左側の子をA[2i ]、右側の子をA[2i +1]とみなすことによって、2分木を表現する。このとき、配列を先頭から順に調べて行くことは、2分木の探索のどれに当たるか。

ア 行きがけ順(先行順)深さ優先探索
イ 帰りがけ順(後行順)深さ優先探索
ウ 通りがけ順(中間順)深さ優先探索
エ 幅優先探索

配列A[1]、A[2]、…、A[n ]でA[1]を根とし、A[i ]の左側の子をA[2i ]、右側の子をA[2i +1]とみなすことによって、2分木を表現する。このとき、配列を先頭から順に調べて行くことは、2分木の探索のどれに当たるか。

ア 行きがけ順(先行順)深さ優先探索
イ 帰りがけ順(後行順)深さ優先探索
ウ 通りがけ順(中間順)深さ優先探索
エ 幅優先探索

解答：エ

＜解説＞

  1. nを7とした場合の2分木の構造は次のようになる。
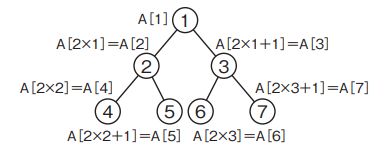
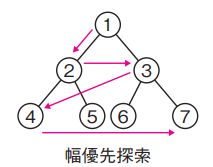
  2. したがって、A[1]→A[2]→A[3]→A[4]・・・という順序で検索することになるため幅優先探索となる。

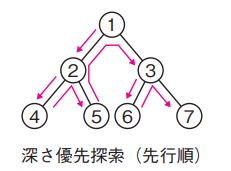
    ※なお深さ優先探索の場合は次のようになる。