次に示すユークリッド互助法(方法1、方法2)で、正の整数a 、b の最大公約数は、それぞれm とn のどちらの変数に求まるか。 ここで、m mod n はm をn で割った余りを表す。

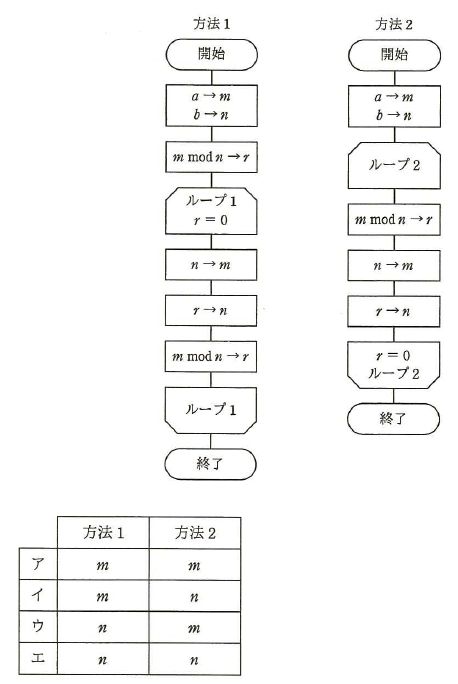
次に示すユークリッド互助法(方法1、方法2)で、正の整数a 、b の最大公約数は、それぞれm とn のどちらの変数に求まるか。 ここで、m mod n はm をn で割った余りを表す。

解答：ウ

＜解説＞

ユークリッド互助法は、2つの整数の割り算を繰り返して最大公約数を求める計算式である。

aの値を35,bの値を30として、トレースする。

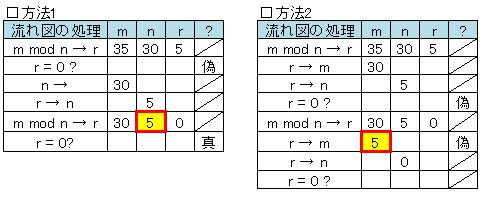
方法1での最大公約数はnに方法2での最大公約数はmとなる。したがって、ウが正解である。

キーワード

• 「ユークリッド互助法」関連の過去問題・・・ユークリッド互助法とは
  • 応用情報技術者 平成27年度(秋季) 問6