2けたの2進数x ₁x ₂が表す整数をx とする。 2進数x ₂x ₁が表す整数を、x の式で表したものはどれか。 ここで、int(r )は非負の実数r の小数点以下を切り捨てた整数を表す。

2けたの2進数x ₁x ₂が表す整数をx とする。 2進数x ₂x ₁が表す整数を、x の式で表したものはどれか。 ここで、int(r )は非負の実数r の小数点以下を切り捨てた整数を表す。

解答：ウ

＜解説＞

2けたの2進数x ₁x ₂が表す整数をx とする。
2進数x ₂x ₁が表す整数を、x の式で表したものはどれか。
ここで、int(r )は非負の実数r の小数点以下を切り捨てた整数を表す。

解答：ウ

＜解説＞

1. 2桁の2進数x ₁x ₂が表す整数xの値と2進数x ₂x ₁が表す整数yの値は次のようになる。
   
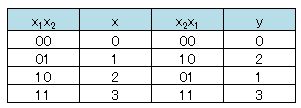
2. 表からyの値はxより1だけ大きいかx以下になることが分かる。アとイの式はyの値が2倍以上になることがあるので、不適切である。
3. ウとエの式の値は次のようになる。
   

したがって、ウが正解である。