- トップページ
- 応用情報技術者
- 平成27年度春季問題一覧
- 平成27年度春季問題1-解答・解説-分析
平成27年度春季問題
問題1
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し、統合後の支店にはATMを1台設置する。
統合後のATMの平均待ち時間を求める式はどれか。
ここで、待ち時間はM/M/1の待ち行列モデルに従い、平均待ち時間にはサービス時間を含まず、ATMを1台に統合しても十分に処理できるものとする。
| [条件] | |
| (1) | 平均サービス時間:Ts |
| (2) | 統合前のシステムの利用率:両支店ともρ |
| (3) | 統合後の利用者数:統合前の両支店の利用者数の合計 |
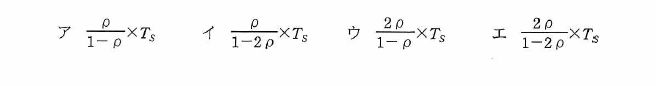
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し、統合後の支店にはATMを1台設置する。
統合後のATMの平均待ち時間を求める式はどれか。
ここで、待ち時間はM/M/1の待ち行列モデルに従い、平均待ち時間にはサービス時間を含まず、ATMを1台に統合しても十分に処理できるものとする。
| [条件] | |
| (1) | 平均サービス時間:Ts |
| (2) | 統合前のシステムの利用率:両支店ともρ |
| (3) | 統合後の利用者数:統合前の両支店の利用者数の合計 |
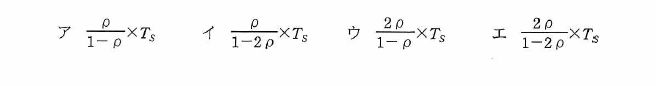
解答:エ
<解説>
- 待ち行列理論のM/M/1モデルでは窓口の平均待ち時間Twは利用率p,平均サービス時間Tsから求められる
Tw = Ts×(p/(1-p)) - 利用率pは平均到着率×平均サービス時間で求められる。統合前の客の人数をλとおくと統合前の利用率pは次のようになる。
p = λ×Ts - 統合後は一つの支店に2支店分の客がくることになるため統合後の利用率p'は次のようになる。
p' = 2λ×Ts =2p
よって、
2p × Ts 1-2p
キーワード
- 「待ち行列理論」関連の過去問題・・・待ち行列理論とは
- 応用情報技術者 平成22年度(春季) 問3
- 応用情報技術者 平成24年度(春季) 問2
- 応用情報技術者 平成27年度(春季) 問1
- 応用情報技術者 平成28年度(春季) 問3
- 高度共通 午前1 平成22年度(春季) 問1
お問い合わせ


