必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 基本情報技術者
  3. 平成23年度特別問題一覧
  4. 平成23年度特別問題2-解答・解説-分析

平成23年度特別問題

問題2

三つの実数X～Zとそれぞれの近似値が次の場合，相対誤差の小さい順に並べたものはどれか。

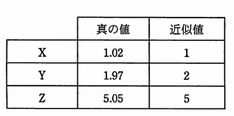
ア X，Y，Z
イ Y，Z，X
ウ Z，X，Y
エ Z，Y，X

三つの実数X～Zとそれぞれの近似値が次の場合，相対誤差の小さい順に並べたものはどれか。

ア X，Y，Z
イ Y，Z，X
ウ Z，X，Y
エ Z，Y，X

解答：エ

＜解説＞

相対誤差は、真の値に対する絶対誤差の割合であり、次の式で求めることができる。

絶対誤差 ＝ |近似値－真の値|
相対誤差 ＝ （絶対誤差）÷真の値

よって

X ： |1－1.02| ÷ 1.02 = 0.02 ÷ 1.02 ≒ 0.019
Y ： |2－1.97| ÷ 1.97 = 0.03 ÷ 1.97 ≒ 0.015
Z ： |5－5.05| ÷ 5.05 = 0.05 ÷ 5.05 ≒ 0.0099

となる。相対誤差の小さい順は「Z,Y,X」となる。