必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. ITパスポート
  3. 平成23年度秋季問題一覧
  4. 平成23年度秋季問題64-解答・解説-分析

平成23年度秋季問題

問題64

1～4の番号をもつ四つの状態がある。四つの状態は図のようにつながれており、時計回りや反時計回りに状態を遷移することができる。

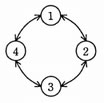
現在、状態1にいて、次の手順を2回実行した後はどの状態にいるか。
[手順]
今いる状態の番号を11倍し、それを3で割った余りによって次の処理を行う。
・余りが0の場合:時計回りに一つ次の状態に遷移する。
・余りが1の場合:反時計回りに一つ次の状態に遷移する。
・余りが2の場合:時計回りに二つ次の状態に遷移する。

ア 1
イ 2
ウ 3
エ 4

1～4の番号をもつ四つの状態がある。四つの状態は図のようにつながれており、時計回りや反時計回りに状態を遷移することができる。

現在、状態1にいて、次の手順を2回実行した後はどの状態にいるか。
[手順]
今いる状態の番号を11倍し、それを3で割った余りによって次の処理を行う。
・余りが0の場合:時計回りに一つ次の状態に遷移する。
・余りが1の場合:反時計回りに一つ次の状態に遷移する。
・余りが2の場合:時計回りに二つ次の状態に遷移する。

ア 1
イ 2
ウ 3
エ 4

解答：エ

＜解説＞

[1回目]

1回目は、状態1にいる。

したがって、1×11＝11, 11÷3＝3 あまり 2となる。

余りが2なので、時計回りに二つ次の状態に遷移する。

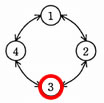
[2回目]

2回目は、状態3にいる。

したがって、3×11＝33, 33÷3＝0 あまり 0となる。

余りが0なので、時計回りに一つ次の状態に遷移する。

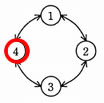
したがって、エが正解となる。