問題13
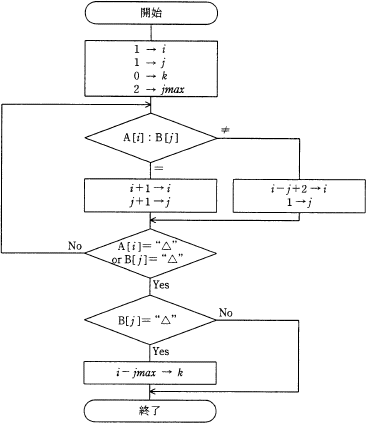
文字列 A が“aababx△”，文字列 B が“ab△”であるとき，流れ図の終了時点の k は幾らか。ここで，文字列の先頭の文字を１番目と数えるものとし，A [ i ] は A の i 番目の文字を，B [ j ] は B の j 番目の文字を，“△”は終端を示す文字を表す。
| ア | 0 |
| イ | 1 |
| ウ | 2 |
| エ | 4 |
解答・解説を見る
解答：ウ
- A[1]＝“a”，B[1]＝“a”なので1回目のA[i]:B[j]の比較で文字列Aと文字列Bの先頭文字aが一致
- i＋1→i=2
- j＋1→j=2
- A[2]＝“a”，B[2]＝“b”なので2回目のA[i]:B[j]の比較で文字列Aと文字列Bの2文字目が不一致
- i－j＋2→i=2
- 1→j→j=1
- A[2]＝“a”，B[1]＝“a”なので3回目のA[i]:B[j]の比較で文字列Aの2文字目aと文字列Bの先頭文字aが一致
- i＋1→i=3，
- j＋1→j=2
- A[3]＝“b”，B[2]＝“b”なので4回目のA[i]:B[j]の比較で文字列Aの3文字目bと文字列Bの2文字目bが一致
- i＋1→i=4，
- j＋1→j=3
- ここでB[3]＝“△”となるので，判定条件A[i]＝“△”orB[j]＝“△”と，次の判定条件B[j]＝“△”の両者を満たし，i－jmax→kの処理に進む。ここでiは4，jmaxは初期値2のままなので，2→kになる。
したがって 、kは文字列Bの先頭文字が一致した文字列Aにおける文字位置を表わしている