必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 応用情報技術者
  3. 平成22年度春季問題一覧
  4. 平成22年度春季問題1-解答・解説-分析

平成22年度春季問題

問題1

0以上255以下の整数nに対して、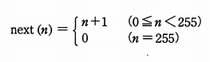



と定義する。next(n)と等しい式はどれか。ここでx AND y及びx OR yは、それぞれxとyを2進数表現にして、けたごとの論理積及び論理和をとったものとする。

ア (n+1)AND 255
イ (n+1)AND 256
ウ (n+1)OR 255
エ (n+1)OR 256

0以上255以下の整数nに対して、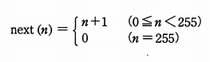



と定義する。next(n)と等しい式はどれか。ここでx AND y及びx OR yは、それぞれxとyを2進数表現にして、けたごとの論理積及び論理和をとったものとする。

ア (n+1)AND 255
イ (n+1)AND 256
ウ (n+1)OR 255
エ (n+1)OR 256

解答：ア

＜解説＞

nが0の場合、next(n)の値はn+1＝1となる。

各選択肢においてnの値を0としたとき、1となるかどうかを検証する。

以上からアのみが1となっている。