- トップページ
- 応用情報技術者
- 平成30年度秋季問題一覧
- 平成30年度秋季問題76-解答・解説-分析
平成30年度秋季問題
問題76
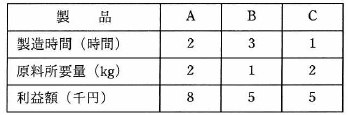
工場で、ある原料から生産している3種類の製品A、B及びCの単位量当たりの製造時間、原料所要量及び利益額を表に示す。 この工場の月間合計製造時間は最大240時間であり、投入可能な原材料は月間150kgである。 このとき、各製品をそれぞれどれだけ作ると最も高い利益が得られるかを求めるのに用いられる手法はどれか。
| ア | 移動平均法 |
| イ | 最小二乗法 |
| ウ | 線形計画法 |
| エ | 定量発注法 |
工場で、ある原料から生産している3種類の製品A、B及びCの単位量当たりの製造時間、原料所要量及び利益額を表に示す。 この工場の月間合計製造時間は最大240時間であり、投入可能な原材料は月間150kgである。 このとき、各製品をそれぞれどれだけ作ると最も高い利益が得られるかを求めるのに用いられる手法はどれか。

| ア | 移動平均法 |
| イ | 最小二乗法 |
| ウ | 線形計画法 |
| エ | 定量発注法 |
解答:ウ
<解説>
線形計画法とは、いくつかの1次式で表わされる制約条件を満たし、かつ1次式で表わされる目的関数を最適化(最大化・最小化)する解を求める数学的手法のこと。主に限られた資源を最大限に利用したい場合、あるいは最小の費用で目的を達成したいような場合、すなわち最適資源配分問題に用いられる。
よって正解はウである。
お問い合わせ


