必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 基本情報技術者
  3. 平成18年度春季問題一覧
  4. 平成18年度春季問題14-解答・解説-分析

平成18年度春季問題

問題14

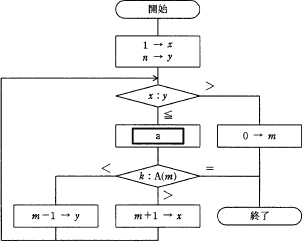
昇順に整列済の配列要素A(1)，A(2)，…，A(n) から，A(m)＝k となる配列要素A(m) の添字 m を2分探索法によって見つける処理を図に示す。終了時点で m＝0 の場合は，A(m)＝k となる要素は存在しない。図中の a に入る式はどれか。ここで，／ は，小数点以下を切り捨てる除算を表す。

ア (x + y) → m
イ (x + y)／2 → m
ウ (x - y)／2 → m
エ (y - x)／2 → m

昇順に整列済の配列要素A(1)，A(2)，…，A(n) から，A(m)＝k となる配列要素A(m) の添字 m を2分探索法によって見つける処理を図に示す。終了時点で m＝0 の場合は，A(m)＝k となる要素は存在しない。図中の a に入る式はどれか。ここで，／ は，小数点以下を切り捨てる除算を表す。

ア (x + y) → m
イ (x + y)／2 → m
ウ (x - y)／2 → m
エ (y - x)／2 → m

解答：イ

＜解説＞

2分探索法は、整列(ソート)済みのデータ列に対して行う探索方法で、データ列の中央の値を見て、検索したい値との大小関係を用いて、検索したい値が中央の値の右にあるか、左にあるかを判断して、探索範囲を狭めながら行っていく方法である。
[　a　] に入る式は，この中間点を求めて添字 m に代入する式である。
ｍは、中央の値になるので、( x ＋ y ) ／2 → m となる。

よってイが正解である。