平成22年度春季解答

問題1

多数のクライアントが、LANに接続された1台のプリンタを共同利用するときの印刷要求から印刷完了までの所要時間を、待ち行列理論を適用して見積もる場合について考える。プリンタの運用方法や利用状況に関する記述のうち、M/M/1の待ち行列モデルの条件に反しないものはどれか。

ア	一部のクライアントは、プリンタの空き具合を見ながら印刷要求をする。
イ	印刷の緊急性や印刷量の多少にかかわらず、到着順に印刷する。
ウ	印刷待ち文章の総量がプリンタのバッファサイズを超えるときは、一時的に受付を中断する。
エ	一つの印刷要求から印刷完了までの所要時間は、印刷の準備に要する一定時間と印刷量に比例する時間の合計である。

解答：イ

＜解説＞

M/M/1モデルでは、次の条件が前提である。

1. 要求がランダムに発生する⇒ポアソン分布
2. 処理時間がランダムである⇒指数分布
3. 窓口は一つである
4. 優先度などの概念はなく到着順に処理される
5. 待ち行列の長さには制限はない

ア	×	1の条件に反する。
イ	○	4の条件と一致する。
ウ	×	5の条件に反する。
エ	×	4の条件に反する。

問題へ

問題2

流れ図は、シフト演算と加算の繰り返しによって、2進整数の乗算を行う手順を表したものである。この流れ図中のa、bの組合せとして、適切なものはどれか。ここで、乗数と被乗数は符号なしの16ビットで表される。X 、Y 、Z は32ビットのレジスタであり、けた送りは論理シフトを用いる。最下位ビットを第0ビットと記す。

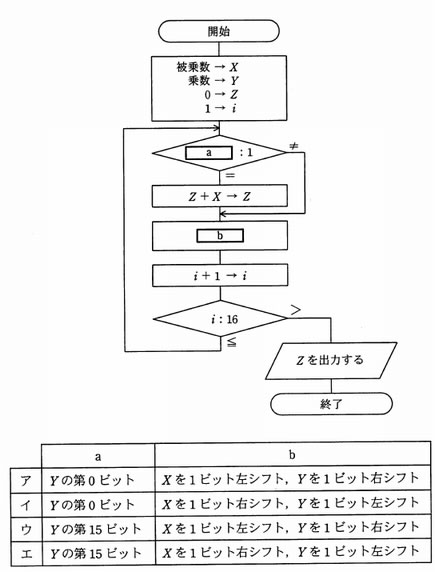
解答：ア

＜解説＞

1. 乗算はシフト演算と加算の組合せで行われる。乗算では1ビット左にシフトすると2倍になる。アまたはウが正解である。
2. 流れ図の最終出力はZである。ZはZ＋X→Zで求められている。したがって、Yの最下位ビット(0ビット)が1ならばZ＋X→Z処理を行う。アが正解である。

問題へ

問題3

整形式(well-formed)のXML文章が妥当(valid)なXML文章である条件はどれか。

ア	DTDに適合している。
イ	XML宣言が完全に記述されている。
ウ	XMLデータを記述するための文法に従っている。
エ	エンティティ参照ができる。

解答：ア

＜解説＞

妥当(valid)なXML文章である条件とは、整形式(well-formed)なXML文書の条件を満たした上で、個別のDTDにも適合したXML文書のことである。

整形式(well-formed)

XMLの仕様が定める基本的規則に適合していることを意味する。

DTD(Document Type Definition：文書型定義)

文書中でどのようなタグや属性が使われているかを定義したものである。
XML文章が文法的に正しくてもデータに欠陥や論理的矛盾がないことは保証できない。そこでDTDによって、そのXML文章が必要とするデータの項目や属性を定義することができる。

ア	○	妥当(valid)なXML文章である条件とは、整形式(well-formed)なXML文書の条件を満たした上で、個別のDTDにも適合したXML文書のことである。
イ	×	整形式のxml文章の条件である。
ウ	×	整形式のxml文章の条件である。
エ	×	エンティティ参照とは、"< "を"&lt;"に">"を"&gt;"といった記号に代用することである。整形式のxml文章の条件である。

問題へ

問題4

ECCメモリで、2ビットの誤りを検出し、1ビットの誤りを訂正するために用いるものはどれか。

ア	偶数パリティ
イ	垂直パリティ
ウ	チェックサム
エ	ハミング符号

解答：エ

＜解説＞

ア	×	偶数パリティとは、同じブロック内の１のビットの数が偶数になるようにパリティビットを付加したもの。１ビットの誤りを検出することができる。
イ	×	垂直パリティとは、同じブロック内の１のビットの数が奇数になるようにパリティビットを付加したもの。１ビットの誤りを検出することができる。
ウ	×	チェックサムチェックサムとは、データを送受信する際の誤り検出方法の一つ。送信前にデータを分割し、それぞれのブロック内のデータを数値とみなして合計を取ったもの。
エ	○	ハミング符号とは、情報を記録する際に、実際のデータに加えてエラーチェック用のコードを付加しておき、読み出したときにそれを検証して、正しいかどうかを判断する技術のこと。 ECC付きメモリーやRAID2などで使われる。2ビットの誤り検出機能と，1ビットの誤り訂正機能を持つ。

問題へ

問題5

あるシステムでは、平均すると100時間に2回の故障が発生し、その都度復旧に2時間を要していた。機器を交換することによって、故 障の発生が100時間で1回になり、復旧に要する時間も1時間に短縮した。機器を交換することによって、このシステムの稼働率は幾ら向上したか。

ア	0.01
イ	0.02
ウ	0.03
エ	0.04

解答：ウ

＜解説＞

稼働率は次式で計算することができる。

	稼働率	=	MTBF
			MTBF+MTTR

MTBF(Mean Time Between Failure：平均故障間隔)

ある機器やシステムが故障するまでの時間の平均値。

MTTR(Mean Time To Repair：平均修理時間)

故障したコンピュータシステムの復旧にかかる時間の平均値。

1. 機器の交換前の稼働率を計算する。
   

   MTBF	＝	100÷2＝50時間
   MTTR	＝	2時間
   稼働率	＝	50÷(50＋2)＝0.961

2. 機器の交換後の稼働率を計算する。

   MTBF	＝	100÷1＝100時間
   MTTR	＝	1時間
   稼働率	＝	100÷(100＋1)＝0.990…

3. 稼働率の向上分を計算する。
   0.99－0.961＝0.03

したがって、ウが正解である。

問題へ