平成23年度特別解答

問題6

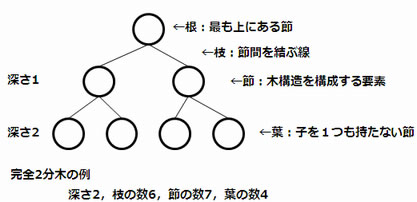
葉以外の節点はすべて二つの子をもち、根から葉までの深さがすべて等しい木を考える。この木に関する記述のうち、適切なものはどれか。ここで、深さとは根から葉に至るまでの枝の個数を表す。

ア	枝の個数がnならば、葉を含む節点の個数もnである。
イ	木の深さが n ならば，葉の個数は 2n-1 である。
ウ	節点の個数がnならば、深さはlog2nである。
エ	葉の個数がnならば、葉以外の節点の個数はn-1である。

解答：エ

＜解説＞

完全二分木（葉以外の節点はすべて二つの子をもち、根から葉までの深さがすべて等しい木）は、次の図のようになる。

ア	×	枝の個数がnならば、葉を含む節点の個数はn+1である。
イ	×	木の深さが n ならば，葉の個数は 2n である。
ウ	×	節点の個数が n ならば，深さは (log2(n+1))-1 である。
エ	○	葉の個数がnならば、葉以外の節点の個数はn-1である。

問題へ

問題7

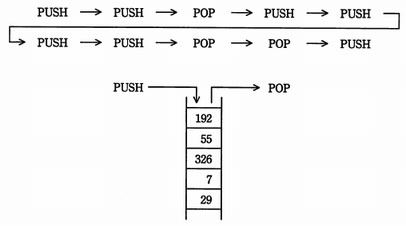
PUSH命令でスタックにデータを入れ、POP命令でスタックからデータを取り出す。動作中のプログラムにおいて、ある状態から次の順で10個の命令を実行したとき、スタックの中のデータは次のようになった。1番目のPUSH命令でスタックに入れたデータはどれか。

ア	29
イ	7
ウ	326
エ	55

解答：イ

＜解説＞

1. PUSHの数は7回，POPの数は3回である。したがって、4個のデータが残ることとなる。
   
2. 問題文の図では、スタックには5個のデータがある。スタックの最下部のデータは既にスタックに存在していたと考えられる。
   
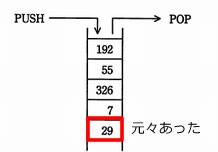
3. 1番目のPUSH命令でスタックにいれたデータは7である。
   

したがって、イが正解である。

問題へ

問題8

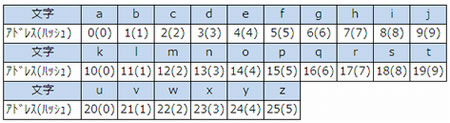
キーが小文字のアルファベット1文字(a,b,・・・,zのいずれか)であるデータを、大きさが10のハッシュ表に格納する。ハッ シュ表として、アルファベットのASCIIコードを10進表記法で表したときの1の位を用いることにする。衝突が起こるキーの組み合わせはどれか。 ASCIIコードは、昇順に連続した2進数が、アルファベット順にコードとして割り当てられている。

ア	aとi
イ	bとr
ウ	cとl
エ	dとx

解答：エ

＜解説＞

ハッシュ表を作成すると、次のようになる。

ア	×	a(0)とi(8)なので衝突しない。
イ	×	b(1)とr(7)なので衝突しない。
ウ	×	c(2)とl(1)なので衝突しない。
エ	○	d(3)とx(3)なので衝突する。

問題へ

問題9

流れ図に示す処理の動作の記述として、適切なものはどれか。ここで、二重線は並列処理の同期を表す。

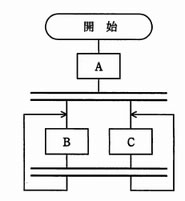
ア	Aの後にBC又はCB、BC又はCB、・・・と繰り返して実行する。
イ	Aの後にBの無限ループ又はCの無限ループになる。
ウ	ABC又はACBを実行してデッドロックになる。
エ	AB又はACを実行してデッドロックになる。

解答：ア

＜解説＞

流れ図に沿って処理をトレースする。

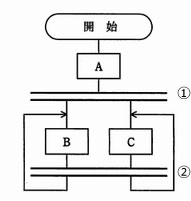
1. Aを実行し、①になる。
2. BかCのどちらかの処理が実行されると、②でもう一方の処理が実行されるのを待つ。
   
3. 両方の処理が終了すると①に戻って2からの処理を繰り返す。
4. A→(BCまたはCB)→(BCまたはCB)…となる。

ア	○	BCまたはCBと繰り返して実行されるので正しい。
イ	×	どちらか一方の無限ループになることはない。
ウ	×	共通資源を使用しているわけではないので、デッドロックにはならない。
エ	×	共通資源を使用しているわけではないので、デッドロックにはならない。

問題へ

問題10

パイプラインの深さをD、パイプラインピッチをP秒とすると、I個の命令をパイプラインで実行するのに要する時間を表す式はどれか。ここで、パイプラインの各ステージは1ピッチで処理されるものとし、パイプラインハザードについては、考慮しなくてよい。

ア	(I+D)×P
イ	(I+D-1)×P
ウ	(I×D)+P
エ	(I×D-1)+P

解答：イ

＜解説＞

パイプラインは，1つの命令の実行サイクルを複数のステージに分割し，各段階の処理を別々の装置が担当することによって，各命令のステージを重ねて，並列実行することにより 1命令あたりの実行効率を上げる方式である。

1. 1命令を処理するのに要する時間は、D×Pである。
2. 2命令を処理するのに要する時間は、前の命令が完了してから1ステップで完了するので(D+1)×Pである。
3. 3命令を処理するのに要する時間は、前の命令が完了してから1ステップで完了するので(D+2)×Pである。
4. 命令を処理するのに要する時間は、{Ｄ＋(Ｉ－1)}×Pで終了する。
5. {Ｄ＋(Ｉ－1)}×P→（イ）(I+D-1)×Pである。

問題へ