必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 応用情報技術者
  3. 平成24年度秋季問題
  4. 平成24年度秋季解答・解説

平成24年度秋季解答

問題1

全体集合S 内に部分集合A とB があるとき、A ∩ B に等しいものはどれか。
ここで、A ∪ B はA とB の和集合、A ∩ B はA とB の積集合、A はS におけるA の補集合、A -B はA からB を除いた差集合を表す。

ア A -B
イ (A ∪ B )-(A ∩ B )
ウ (S -A ) ∪ (S -B )
エ S -(A ∩ B )

解答：ア

＜解説＞

論理式A ∩ B をベン図で表現すると次のようになる。

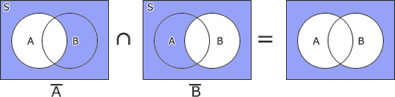
ア～エの論理式をベン図で表すと次の様になる。

ア ○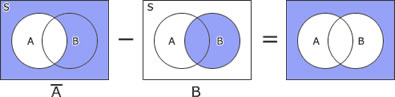
イ ×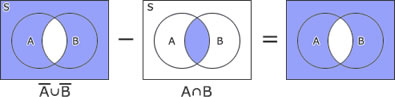
ウ ×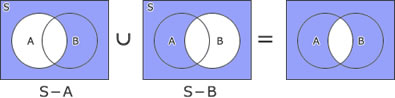
エ ×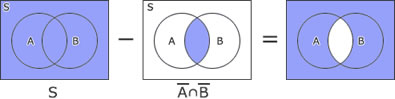

したがって、アが正解である。

問題へ

問題2

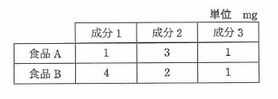
食品A及び食品Bの各1gに含まれる三つの成分1～3を調べたところ、含有量は表のようになった。 成分1を70mg以上、成分2を80mg以上摂取するとき、成分3の最小摂取量は何mgか。

ア 28
イ 31
ウ 32
エ 34

解答：イ

＜解説＞

  1. 成分1を70mg以上、摂取することから食品Aの量をX，食品Bの量をYとすると、①X+Y=70となる。
  2. 成分2を80mg以上、摂取することから食品Aの量をX，食品Bの量をYとすると、②3X+2Y=80となる。
  3. ①②を連立方程式としてXとYを求める。②を2倍し、
    X+4Y=70,6X+4Y=160
    ⇒5x=90,X=18となる。
  4. Xの値を①に代入する
    18+4Y=70,4Y=52,Y=13
  5. 食品Aを18g，食品Bを13gというのが最小摂取量を得るための食品量となる。
  6. 成分3はそれぞれの食品1gあたり1mg含まれているので、
    18+13=31mgとなる。

したがって、イが正解である。

問題へ

問題3

4ビットから成る情報ビットx1x2x3x4に対して、
　(x 1 + x 2 + x 3 + x 5) mod 2 = 0
　(x 1 + x 2 + x 4 + x 6) mod 2 = 0
　(x 2 + x 3 + x 4 + x 7) mod 2 = 0
を満たす冗長ビットx 5x 6x 7を付加した符号x 1x 2x 3x 4x 5x 6x 7を送信する。
受信符号y 1y 2y 3y 4y 5y 6y 7が、送信符号と高々1ビットしか異ならないとき、
　(y 1 + y 2 + y 3 + y 5) mod 2
　(y 1 + y 2 + y 4 + y 6) mod 2
　(y 2 + y 3 + y 4 + y 7) mod 2
がそれぞれ0になるかどうかによって、正しい情報ビットx 1x 2x 3x 4x を求めることが可能である。
y 1y 2y 3y 4y 5y 6y 7 = 1100010であるとき、正しい情報ビットはどれか。
ここで、a mod b は、a を b で割った余りを表す。

ア 0100
イ 1000
ウ 1100
エ 1101

解答：エ

＜解説＞

受信ビット列y 1y 2y 3y 4y 5y 6y 7＝ 1100010を式に代入し、その正誤を確認する。

値を代入した結果、式2と式3が誤りとなる。

したがって、式2と式3に共通に含まれるy 4が誤って伝えられた情報ビットであると特定できる。

それに伴いy 4=0→1となり正しい情報ビット列は1101となる。

よってエが正解である。

問題へ

問題4

式E = (A + B)×(C - D)と対応する逆ポーランド表記法はどれか。

ア =E×+AB-CD
イ EAB+CD-×=
ウ EAB-CD+×=
エ EABC×+D-=

解答：イ

＜解説＞

逆ポーランド表記法とは、数式やプログラムを記述する方法。演算子を被演算子の後に記述することから、後置記法とも言う。

式E = (A + B)×(C - D)は次のように変換される。

  1. (E=((A+B)×(C-D)))
  2. (E=((AB+)×(CD-)))
  3. (E=((AB+)(CD-)×))
  4. (E((AB+)(CD-)×)=)
  5. EAB+CD-×=

したがってイが正解である。

問題へ

問題5

配列を用いてスタックを実現する場合の構成要素として、最低限必要なものはどれか。

ア スタックに最後に入った要素を示す添字の変数
イ スタックに最初に入った要素と最後に入った要素を示す添字の変数
ウ スタックに一つ前に入った要素を示す添字の変数を格納する配列
エ スタックの途中に入っている要素を示す添字の変数

解答：ア

＜解説＞

スタックとは、ある場所に格納したデータを、新しく格納した順に取り出すようにする方式。一番古く格納されたデータが一番最後に取り出される、LIFO（Last In, First Out：後入れ先出し）型のバッファのことである。

  1. スタックに新しい値を格納する場合は、最後に値が格納された領域の1つ上の領域に格納する。
  2. 新しい値の格納により最後に値が格納された領域が一つ上に移動する。
  3. スタックから値を取り出すときは、最後に値が格納された領域から取り出す。
  4. 値を取り出すことにより最後に値が格納された領域の位置が１つ下に移動する。

したがって、スタックへの値の出し入れを表現するには、最低でも最後に値が格納された領域を示す添え字を用いればよい。したがってアが正解である。

問題へ