平成24年度秋季問題
問題1
全体集合S 内に部分集合A とB があるとき、A ∩ B に等しいものはどれか。
ここで、A ∪ B はA とB の和集合、A ∩ B はA とB の積集合、A はS におけるA の補集合、A -B はA からB を除いた差集合を表す。
| ア | A -B |
| イ | (A ∪ B )-(A ∩ B ) |
| ウ | (S -A ) ∪ (S -B ) |
| エ | S -(A ∩ B ) |
問題2
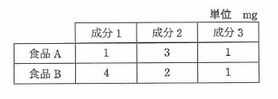
食品A及び食品Bの各1gに含まれる三つの成分1~3を調べたところ、含有量は表のようになった。 成分1を70mg以上、成分2を80mg以上摂取するとき、成分3の最小摂取量は何mgか。
| ア | 28 |
| イ | 31 |
| ウ | 32 |
| エ | 34 |
問題3
4ビットから成る情報ビットx1x2x3x4に対して、
(x 1 + x 2 + x 3 + x 5) mod 2 = 0
(x 1 + x 2 + x 4 + x 6) mod 2 = 0
(x 2 + x 3 + x 4 + x 7) mod 2 = 0
を満たす冗長ビットx 5x 6x 7を付加した符号x 1x 2x 3x 4x 5x 6x 7を送信する。
受信符号y 1y 2y 3y 4y 5y 6y 7が、送信符号と高々1ビットしか異ならないとき、
(y 1 + y 2 + y 3 + y 5) mod 2
(y 1 + y 2 + y 4 + y 6) mod 2
(y 2 + y 3 + y 4 + y 7) mod 2
がそれぞれ0になるかどうかによって、正しい情報ビットx 1x 2x 3x 4x を求めることが可能である。
y 1y 2y 3y 4y 5y 6y 7 = 1100010であるとき、正しい情報ビットはどれか。
ここで、a mod b は、a を b で割った余りを表す。
| ア | 0100 |
| イ | 1000 |
| ウ | 1100 |
| エ | 1101 |
問題4
式E = (A + B)×(C - D)と対応する逆ポーランド表記法はどれか。
| ア | =E×+AB-CD |
| イ | EAB+CD-×= |
| ウ | EAB-CD+×= |
| エ | EABC×+D-= |
問題5
配列を用いてスタックを実現する場合の構成要素として、最低限必要なものはどれか。
| ア | スタックに最後に入った要素を示す添字の変数 |
| イ | スタックに最初に入った要素と最後に入った要素を示す添字の変数 |
| ウ | スタックに一つ前に入った要素を示す添字の変数を格納する配列 |
| エ | スタックの途中に入っている要素を示す添字の変数 |
お問い合わせ


