平成16年度春季解答

問題1

10 進数の演算式 7 ÷ 32 の結果を 2 進数で表したものはどれか。

ア	0.001011
イ	0.001101
ウ	0.00111
エ	0.0111

解答：ウ

＜解説＞

1. 7÷32を計算する。
   7÷32 = 0.21875
2. 0.21875を2進数に変換する。

よって0.00111が解答である。

問題へ

問題2

次の式は、何進法で成立するか。

1015 ÷ 5 = 131 (余り 0)

ア	6
イ	7
ウ	8
エ	9

解答：イ

＜解説＞

n進数の整数部のm桁目は、10進数では、nの(m-1)乗の重みを持つ。

従って、1015が1～4の選択肢の進法であるとすると、その値を10進数で表した値はそれぞれ、

• 1×6³＋0×6²＋1×6¹＋5×6⁰ ・1×7³＋0×7²＋1×7¹＋5×7⁰
• 1×8³＋0×8²＋1×8¹＋5×8⁰ ・1×9³＋0×9²＋1×9¹＋5×9⁰

となる。

問題の式は、5で割ったときの余りが0であるので、項目2か項目3が正解であることがわかる。項目2、項目3の式を5で割るとそれぞれ次のようになる。

• 355÷5=71=131₍₇₎
• 525÷5=105=151₍₈₎

問題へ

問題3

実数 a を a = f × r^e と表す浮動小数点表記に関する記述として、適切なものはどれか。

ア	f を仮数、e を指数、r を基数という。
イ	f を基数、e を仮数、r を指数という。
ウ	f を基数、e を指数、r を仮数という。
エ	f を指数、e を基数、r を仮数という。

解答：ア

＜解説＞

a = f × r^e と表す浮動小数点表記に関する記述では、fを仮数、eを指数、rを基数という。
浮動小数点表記では、数値を次のような形式で表す。

(仮数)×(基数)^指数

問題へ

問題4

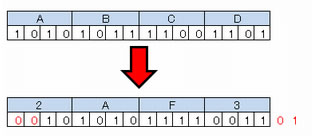
32 ビットのレジスタに 16 進数 ABCD が入っているとき、2 ビットだけ右に論理シフトしたときの値はどれか。

ア	2AF3
イ	6AF3
ウ	AF34
エ	EAF3

解答：ア

＜解説＞

論理シフトで右にシフトした場合，あふれたビットは捨てられ，空いたビットに0が入る。

問題へ

問題5

けた落ちの説明として、適切なものはどれか。

ア	値がほぼ等しい浮動小数点同士の減算において、有効けた数が大幅に減ってしまうことがある。
イ	演算結果が、扱える数値の最大値を超えることによって生じる誤差である。
ウ	数表現のけた数に限度があるとき、最小のけたより小さい部分について四捨五入、切上げ又は切捨てを行うことによって生じる誤差である。
エ	浮動小数点の加算において、一方の数値の下位のけたが欠落することである。

解答：ア

＜解説＞

ア	○	けた落ちに関する説明である。
イ	×	けたあふれ(オーバーフロー)に関する説明である。
ウ	×	丸め誤差に関する説明である。
エ	×	情報落ちに関する説明である。

問題へ