平成16年度春季解答

問題6

赤、白、黄の 3 種類の球が 3 個ずつ入っている箱の中から、3 個の球を同時に取り出すとき、すべて白の球になる確率は幾らか。

ア	1/84
イ	3/14
ウ	5/21
エ	11/14

解答：ア

＜解説＞

1. 1個目の球が白の確率は、9個の中から3つで3/9＝1/3
2. 2個目の球が白の確率は、8個の中から2つで、2/8＝1/4
3. 3個目の球が白の確率は、7個の中から1つで、１/７
4. 全体の確率＝1/3×1/4×1/7＝1/84

問題へ

問題7

1 ビットの数 A、B の和を 2 ビットで表現したとき、上位ビット C と下位ビット S を表す論理式の組合せはどれか。ここで、"・"は論理積、"＋"は論理和、Xは X の否定を表す。

解答：ア

＜解説＞

• 上位ビットCはA，Bがともに1のときだけ1となる。よってCはAとBの論理積A・Bで表される。
• 下位ビットSはA，Bの論理値が互いに異なる場合だけ1となる。よってSはAとBの排他的論理和で表される。

問題へ

問題8

関数 eq(X,Y) は、引数 X と Y の値が等しければ 1 を返し、異なれば 0 を返す。整数 A、B、C について、eq(eq(A,B),eq(B,C)) を呼び出したとき、1 が返ってくるための必要十分条件はどれか。

ア	(A = B かつ B = C) 又は (A ≠ B かつ B ≠ C)
イ	(A = B かつ B = C) 又は (A ≠ B 又は B ≠ C)
ウ	（ A ＝ B かつ B ＝ C ）又は A ＝ C
エ	(A = B 又は B = C) 又は A = C

解答：ア

＜解説＞

eq(eq(A,B)，eq(B,C))が１を返すのは、①eq(A,B)とeq(B,C)がどちらも１を返す場合または②eq(A,B)とeq(B,C)がどちらも0を返す場合である。
①になるための条件はA＝BかつB＝C，②こなるための条件はA≠BかつB≠Cなので，全体の必要条件は｢①または②である。

正解はアである。

問題へ

問題9

論理型の変数 A ， B の値にかかわらず，次の流れ図と同一の分岐が得られるものはどれか。ここで，AND は論理積，OR は論理和，XOR は排他的論理和，NAND は否定論理積を表す。

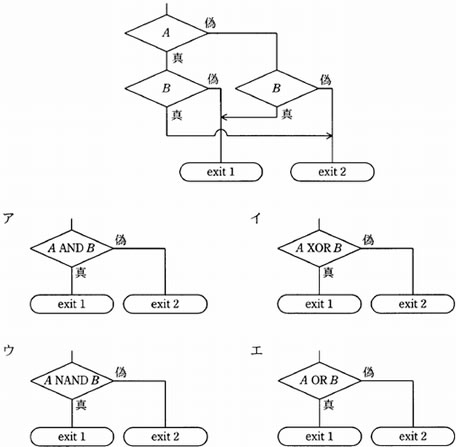
解答：イ

＜解説＞

流れ図の結果は、次の4通りである。

A：偽,B：偽 = exit2

A：偽,B：真 = exit1

A：真,B：偽 = exit1

A：真,B：真 = exit2

ア	×	A が真、B が真の場合にexit１となる。
イ	○	上記式より正しい。
ウ	×	A が偽、B が偽の場合にexit１となる。
エ	×	A が真、B が真の場合にexit１となる。

問題へ

問題10

2 種類の文字 "A"、"B" を 1 個以上、最大 n 個並べた符号を作る。60 通りの符号を作るときの n の最小値は幾らか。

ア	4
イ	5
ウ	6
エ	7

解答：イ

＜解説＞

文字A,Bをn個並べたとき、表せる符合の数は、2ⁿ通りとなる。従って、60通りの符号を表すnの最小値は、
2¹＋2²＋2³＋2⁴＋2⁵=62
となる。したがって、5である。

問題へ