平成20年度秋季解答

問題1

次の流れ図は，10 進整数 j （0 ＜ j ＜ 100 ）を8けたの2進数に変換する処理を表している。2進数は下位けたから順に，配列の要素 NISHIN (1) から NISHIN (8) に格納される。流れ図の a 及び b に入る処理はどれか。ここで， j div 2は j を2で割った商の整数部分を， j mod 2は j を2で割った余りを表す。

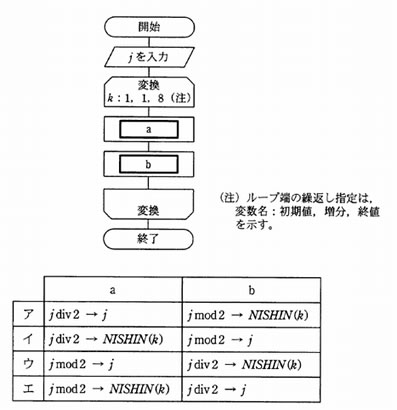
解答：エ

＜解説＞

10進数を2進数に変換するには，次の手順で行う。

1. 10進数を2で割った余りを2進数の各けたに順番にセット
   j mod 2 → NISHIN[k]
2. 10進数を2で割った商を求める
   j div 2 →j
3. 1に戻り繰り返す

空欄aが1の処理，空欄bが②の処理に対応する。
よってエが正解である。

問題へ

問題2

基数変換に関する記述のうち，適切なものはどれか。

ア	2進数の有限小数は，10 進数にしても必ず有限小数になる。
イ	8進数の有限小数は，2進数にすると有限小数にならないこともある。
ウ	8進数の有限小数は，10 進数にすると有限小数にならないこともある。
エ	10 進数の有限小数は，8進数にしても必ず有限小数になる。

解答：ア

＜解説＞

ア	○	8進数の有限小数は，10 進数にしても必ず有限小数になる。
イ	×	8進数の有限小数は，2進数にしても必ず有限小数になる。
ウ	×	8進数の有限小数は，10 進数にしても必ず有限小数になる。
エ	×	10進数の有限小数は，8進数にすると有限小数にならないこともある。

問題へ

問題3

2の補数で表された負数 10101110 の絶対値はどれか。

ア	01010000
イ	01010001
ウ	01010010
エ	01010011

解答：ウ

＜解説＞

1. 各ビットを反転する。
   10101110→01010001
2. 1を加算する。
   01010001→01010010
   

問題へ

問題4

浮動小数点演算において，絶対値の大きな数と絶対値の小さな数の加減算を行ったとき，絶対値の小さな数の有効けたの一部又は全部が結果に反映されないことを何というか。

ア	打切り誤差
イ	けた落ち
ウ	情報落ち
エ	絶対誤差

解答：ウ

＜解説＞

ア	×	打ち切り誤差は、浮動小数点の計算処理の打ち切りを指定した規則で行うことによって発生する誤差（無限小数を打ち切る場合など）である。
イ	×	けた落ちは、値の近い数値の減算で有効数字のけた数が激減することである。
ウ	○	情報落ちは、絶対値の大きな数と絶対値の小さな数の加減算を行ったとき，絶対値の小さな数の有効けたの一部又は全部が結果に反映されないことである。
エ	×	絶対誤差は、演算結果と正しい値（真値）との差のことである。

問題へ

問題5

実数 a を引数とする関数 int( a ) は， a を超えない最大の整数値を返す。たとえば，
　　int(8.9)＝8
　　int(-8.5)＝－9
である。整数 b と正の小数 c （0＜ c ＜1 ）に対して，
　　a ＝-（ b ＋ c ）
が成り立つとき，
　　a -int（ a ）
を c を使って表した式はどれか。

ア	c
イ	-c
ウ	1-c
エ	c-1

解答：ウ

＜解説＞

1. a = - (b+c)に8.9を代入する。

   8.9

   ＝

   - (b+c)

   bは整数かつ0＜ c ＜1なのでb=-9，c=0.1となる。
2. a －int（ a ）に8.9を代入する。

   8.9-int(8.9)	＝	8.9-8
   	＝	0.9

3. a －int（ a ）=0.9，c=0.1より a －int（ a ）をcを使った式で表すと1-cとなる。

問題へ