- トップページ
- 基本情報技術者
- 平成20年度秋季問題
- 平成20年度秋季解答・解説
平成20年度秋季解答
問題6
0~9の数字と空白文字を組み合わせて長さ3の文字列を作る。先頭1文字には数字を使えるが,空白文字は使えない。2文字目以降には空白文字も使えるが,空白文字の後に数字を並べることは許されない。何通りの文字列を作ることができるか。ここで,同じ数字の繰返し使用を許すものとする。
| ア | 1110 |
| イ | 1111 |
| ウ | 1210 |
| エ | 1331 |
解答:ア
<解説>
- 先頭1文字目が0,1,…,9のいずれかで,2文字目以降が空白の場合→10通り
- 先頭1文字目と2文字目が0,1,…,9のいずれかで,3文字目が空白の場合→10×10=100通り
- 先頭1文字目,2文字目,3文字目が0,1,…,9のいずれかである場合→10×10×10=1000通り
- 1~3の合計を求める。10+100+1000=1110通りである。
問題7
図の線上を,点 P から点 R を通って,点 Q に至る最短経路は何通りあるか。
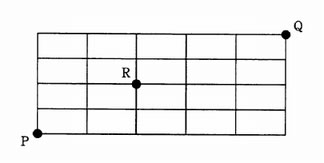
| ア | 16 |
| イ | 24 |
| ウ | 32 |
| エ | 60 |
解答:エ
<解説>
- PからRまでの最短経路を計算する。
「↑↑→→」、「↑→↑→」、「↑→→↑」、「→↑↑→」、「→↑→↑」、「→→↑↑」
- RからQまでの最短経路を計算する。
「↑↑→→→」、「↑→↑→→」、「↑→→↑→」、「↑→→→↑」、「→↑↑→→」、
「→↑→↑→」、「→↑→→↑」、「→→↑↑→」、「→→↑→↑」、「→→→↑↑」 - 全体の経路を計算する。
6×10=60
問題8
5本のくじがあり,そのうち2本が当たりである。くじを同時に2本引いたとき,2本とも当たりとなる確率は幾らか。
| ア |
|
||
| イ |
|
||
| ウ |
|
||
| エ |
|
解答:ウ
<解説>
| 5本のくじのうち2本が当たりなので、1本目が当たる確率は、 | 2 | である。 |
| 5 |
| 残った4本のうち1本が当たりなので、2本目が当たる確率は、 | 1 | である。 |
| 4 |
| よって2本とも当たりとなる確率は、 | 2 | × | 1 | = | 2 | = | 1 | である。 |
| 5 | 4 | 20 | 10 |
問題9
関数 eq(X,Y) は、引数 X と Y の値が等しければ 1 を返し、異なれば 0 を返す。整数 A、B、C について、eq(eq(A,B),eq(B,C)) を呼び出したとき、1 が返ってくるための必要十分条件はどれか。
| ア | (A = B かつ B = C) 又は (A ≠ B かつ B ≠ C) |
| イ | (A = B かつ B = C) 又は (A ≠ B 又は B ≠ C) |
| ウ | (A = B かつ B = C) 又は (A ≠ B かつ B ≠ C) |
| エ | (A = B 又は B = C) 又は A = C |
解答:ア
<解説>
eq(eq(A,B),eq(B,C))が1を返すのは、①eq(A,B)とeq(B,C)がどちらも1を返す場合または②eq(A,B)とeq(B,C)がどちらも0を返す場合です。
①になるための条件はA=BかつB=C,②こなるための条件はA≠BかつB≠Cなので,全体の必要条件は「①または②である。
正解はアである。
問題10
次の真理値表の演算結果を表す論理式はどれか。ここで,+は論理和,・は論理積を表す。
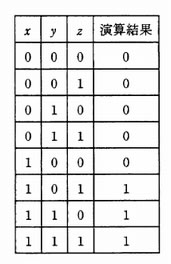
| ア | (x ・ y) + z |
| イ | (x + y) ・ z |
| ウ | x ・ (y + z) |
| エ | x + (y ・ z) |
解答:ウ
<解説>
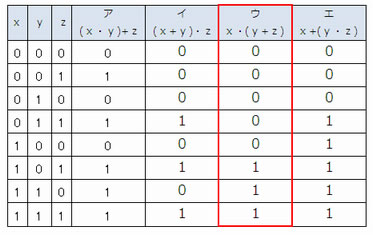
よってウが正解である。
お問い合わせ


