平成20年度秋季解答

問題11

0～6の数4個で構成される数列（ N ₃， N ₂， N ₁， C ）がある。 C はチェックディジット（検査数字）であり、 C ＝（ N ₃×3＋ N ₂×2＋ N ₁×1） mod 7を満たす。数列（ 4，2，□，6）がこの条件を満たすとき、□ に当てはまる数はどれか。ここで、 a mod b は a を b で割った余りを表す。

ア	0
イ	2
ウ	4
エ	6

解答：ウ

＜解説＞

　N₃＝4，N₂＝2，C＝6なので，（4×3＋2×2＋N₁×1） mod 7＝6
　（16＋N₁） mod 7＝6，すなわち（16＋N₁）を7で割った剰余が6になる。
　N₁は0～6の数なので，N₁＝4である。

問題へ

問題12

親の節の値が子の節の値より小さいヒープがある。このヒープへの挿入は，要素を最後部に追加し，その要素が親よりも小さい間，親と子を交換することを繰り返せばよい。次のヒープの * の位置に要素７を追加したとき，A の位置に来る要素はどれか。

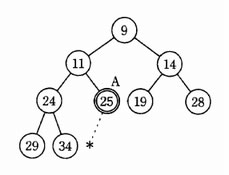
ア	7
イ	11
ウ	24
エ	25

解答：イ

＜解説＞

下図のように、11がA の位置に来る。

問題へ

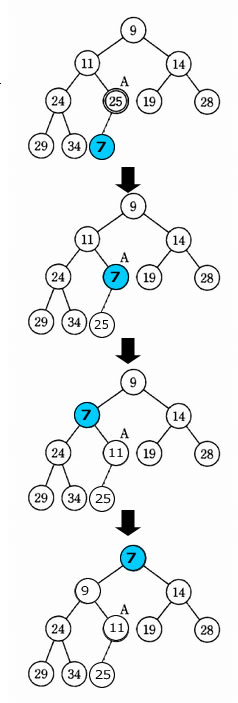
問題13

2,000 個の相異なる要素が，キーの昇順に整列された表がある。外部から入力したキーによってこの表を2分探索して，該当するキーの要素を取り出す。該当するキーが必ず表中にあることが分かっているとき，キーの比較回数は最大何回か。

ア	9
イ	10
ウ	11
エ	12

解答：ウ

＜解説＞

2分探索の場合，1回の探索を行うごとに探索するデータ範囲の要素の個数が半分(1／2)になる。データの個数が2,000個であれば、比較するごとに、データの個数が2000個であれば比較するごとに①1000,②500,③250,④125,⑤63,⑥32,⑦16,⑧8,⑨4,⑩2,⑪1のように減っていくので、最大でも11回の比較で目的のデータは見つかる。

問題へ

問題14

n の階乗を再帰的に計算する関数 F（ n）の定義において，a に入れるべき式はどれか。ここで，n は非負の整数である。
　n ＞0のとき， F（n）＝ a
　n ＝０のとき， F（n）＝ 1

ア	n + F(n -1)
イ	n - 1 + F(n)
ウ	n × F(n -1)
エ	(n - 1) × F(n)

解答：ウ

＜解説＞

n の階乗は、n=n…3×2×1 となる。 （例：5 の階乗は、 5×4×3×2×1。）

したがってn の階乗 F（n）は、

F（n）	＝	n × n －1 × n －2 × n － 3… × 1
	＝	n ×F（n - 1）

となる。

問題へ

問題15

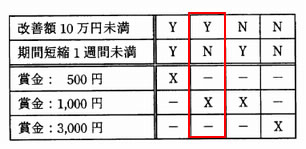
業務の改善提案に対する賞金が，次の決定表で決められる。改善提案１と改善提案2に対する賞金の総額は何円か。

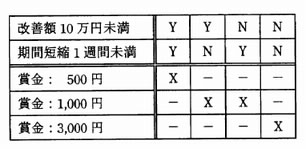
[改善提案]
改善提案１：	改善額 20万円	, 期間短縮 3日
改善提案２：	改善額 5万円	, 期間短縮 2週間

ア	1,000
イ	1,500
ウ	2,000
エ	3,500

解答：ウ

＜解説＞

改善提案1

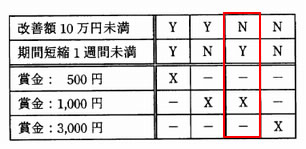
改善提案1は、改善額10万円未満＝Ｎ。期間短縮1週間未満＝Ｙ。
よって下図より、賞金は1,000円である。

改善提案2

改善提案2は、改善額10万円未満＝Ｙ。期間短縮1週間未満＝Ｎ。
よって下図より、賞金は1,000円である。

問題へ