平成23年度秋季解答

問題1

16 ビットの2進数 n を 16 進数の各けたに分けて，下位のけたから順にスタックに格納するために，次の手順を4回繰り返す。a，b に入る適切な語句の組合せはどれか。ここで，xxxx16 は 16 進数 xxxx を表す。

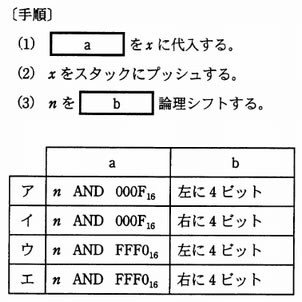
解答：イ

＜解説＞

1. 【　a　】は、下位4ビットを取り出す処理である。下位4ビットを取り出す為には、n に 000F₁₆をマスクする必要がある。
   
2. ｘをスタックにプッシュする。
3. nを右に4ビット論理シフトする。最下位の4ビットのビットパターンが除かれて次の桁の4ビットの取り出しの準備できる。
   

問題へ

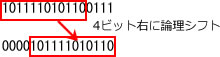
問題2

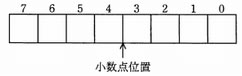
10進数-5.625を，8ビット固定小数点形式による2進数で表したものはどれか。ここで，小数点位置は3ビット目と4ビット目の間とし，負数には2の補数表現を用いる。

ア	01001100
イ	10100101
ウ	10100110
エ	11010011

解答：ウ

＜解説＞

1. 10 進数 -5.625 を2進数に変換する。整数部分は5であるから 101 となる。小数部分は次の計算より101となる。
   
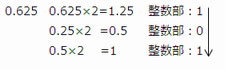
   よって、10 進数 5.625 は2進数で 101.101 となる。
   
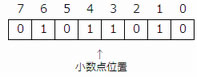
2. 負数は2の補数表現を用いるので、2の補数を計算する。
   
   
   

問題へ

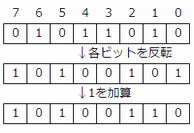
問題3

コンピュータで連立一次方程式の解を求めるのに、式に含まれる未知数の個数の3乗に比例する計算時間が掛かるとする。あるコンピュータで 100 元連立一次方程式の解を求めるのに2秒掛かったとすると、その4倍の演算速度をもつコンピュータで 1,000 元連立一次方程式の解を求めるときの計算時間は何秒か。

ア	5
イ	50
ウ	500
エ	5,000

解答：ウ

＜解説＞

100 元連立一次方程式の解を求めるのに2秒かかる場合、1,000 元連立一次方程式の解を求めるときの計算時間を計算する。この場合、「未知数の個数の3乗に比例する」と指定されているので、計算時間を x 秒 とすると次のようになる。

x	=	2 × 10003 ÷ 1003
	=	2000(秒)

4倍の演算速度をもつコンピュータで計算した場合は、計算時間は4分の1になるので 500(秒)となる。

問題へ

問題4

次の規則から生成することができる式はどれか。

〔規則〕
＜式＞ ::＝＜変数＞｜（＜式＞＋＜式＞）｜＜式＞＊＜式＞
＜変数＞ ::＝A｜B｜C｜D

ア	A + (B + C) * D
イ	(A + B) + (C + D)
ウ	(A + B) * (C + D)
エ	(A * B) + (C * D)

解答：ウ

＜解説＞

式の形式は次の3種類である。

• ＜変数＞
• (＜式＞＋＜式＞)
• ＜式＞＊＜式＞

生成規則から次のことが分かる。

• ＋は、(＜式＞＋＜式＞）のように、かっこでくくられる。
• ＊は、＜式＞＊＜式＞のように、かっこでくくられない
  

よって、

となる。

問題へ

問題5

スタック1，2があり，図の状態になっている。関数f はスタック1からポップしたデータをそのままスタック2にプッシュする。関数g はスタック2からポップしたデータを出力する。b，c，d ，a の順番に出力するためには，関数をどの順で実行すればよいか。

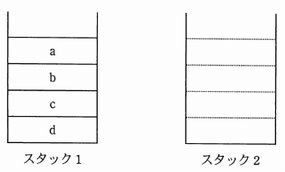
ア	f,f,g,f,f,g,g,g
イ	f,f,g,f,g,f,g,g
ウ	f,f,g,f,g,g,f,g
エ	f,f,g,g,f,f,g,g

解答：イ

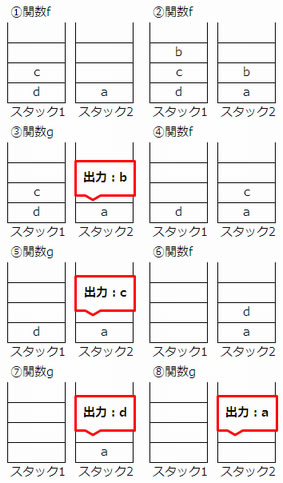
＜解説＞

下図より、f,f,g,f,g,f,g,gの順に関数を実行する必要がある。

問題へ