平成26年度秋季解答

問題1

A、B、C、Dを論理変数とするとき、次のカルノー図と等価な論理式はどれか。ここで、・は論理積、+は論理和、XはXの否定を表す。

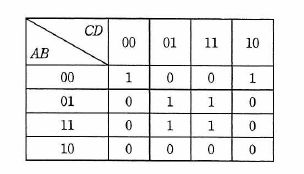s

ア	A・B・C・D + B・D
イ	A・B・C・D + B・D
ウ	A・B・D + B・D
エ	A・B・D + B・D

解答：エ

＜解説＞

カルノー図の出力が1のところを丸で囲むと下の図のようになる。

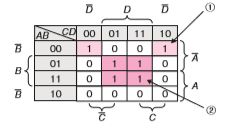
①の囲いは、A = 0かつB = 0かつD = 0であれば、Cの0・1には影響しないので、A・B・D(①)になる。
②の囲いは、B = 1かつD = 1であれば、AとCの0・1には影響しないので、B・D(②)になる。
したがって、出力の式は① + ②なので、A・B・D + B・D(エ)になる。

問題へ

問題2

コンピュータによる伝票処理システムがある。このシステムは、伝票データをためる待ち行列をもち、M/M/1の待ち行列モデルが適用できるものとする。平均待ち時間がT 秒以上となるのは、処理装置の利用率が少なくとも何%以上となったときか。ここで、伝票データをためる待ち行列の特徴は次のとおりである。

• 伝票データは、ポアソン分布にしたがって発生する。
• 伝票データのたまる数に制限はない。
• 1件の伝票データの処理時間は、平均T 秒の指数分布に従う。

ア	33
イ	50
ウ	67
エ	80

解答：イ

＜解説＞

1. 処理装置の利用率をpとすると待ち行列の長さは、p/(1-p)で表すことができる。
   平均待ち時間 (Tw)=待ちぎょうれうの長さ×平均処理時間(Ts)

   Tw	＝	p	Ts
   		(1-p)

2. 平均回線待ち時間が平均伝送時間よりも最初に長くなるのはTwとTsが等しい場合のので、Tw=Ts=Tの時を考えると

   T	＝	p	T
   		(1-p)

3. 両辺をTで割ると次のようになる
   1=p/(1-p)
   1-p=p
   2p=1
   p=0.5 ∴50%

問題へ

問題3

V ₅、V ₆、V ₄

解答：イ

＜解説＞

ダイクストラ法を用いて最短経路を求めると次のようになる。

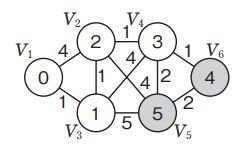
したがって、V ₄、V ₆、V ₅となる。

問題へ

問題4

キャッシュの書込み方式には、ライトスルー方式とライトバック方式がある。 ライトバック方式を使用する目的として、適切なものはどれか。

キャッシュの書込み方式には、ライトスルー方式とライトバック方式がある。ライトバック方式を使用する目的として、適切なものはどれか

ア	キャッシュと主記憶の一貫性(コヒーレンシ)を保ちながら、書込みを行う。
イ	キャッシュミスが発生したときに、キャッシュの内容の主記憶への書き戻しを不要にする。
ウ	個々のプロセッサがそれぞれのキャッシュをもつマルチプロセッサシステムにおいて、キャッシュ管理を簡単な回路構成で、実現する。
エ	プロセッサから主記憶への書込み頻度を減らす。

解答：エ

＜解説＞

書込み命令が実行された時に、キャッシュメモリと主記憶の両方を書き換える方式のことを、ライトスルー方式(write through) ，キャッシュメモリだけを書き換えておき、主記憶の書き換えはブロックの入れ替え時に行う方式のことを、ライトバック(write back) 方式という。

ライトスルー方式

• キャッシュへの書込みと同時に主記憶にも書き込む方式
• キャッシュと主記憶の一貫性(コヒーレンシ)は常に保たれる
• 書き込みの高速化はできない

ライトバック方式

• キャッシュから追い出された時点で主記憶へ書き込む方式
• 主記憶への書込みが終了するまでキャッシュとの一貫性(コヒーレンシ)が保たれない
• 書込みも高速化できる

ア	×	ライトスルー方式の説明である。ライトバック方式では、キャッシュと主記憶の一貫性(コヒーレンシ)が保たれないことがある。
イ	×	ライトスルー方式の説明である。ライトバック方式では、キャッシュミスが発生したとき、キャッシュの内容を主記憶に書き戻す必要がある。
ウ	×	ライトスルー方式の説明である。ライトバック方式では、個々のプロセッサのもつキャッシュと主記憶の一貫性を調整するため回路構成は複雑になる。
エ	○	ライトバック方式の説明である。ライトバック方式では、プロセッサが主記憶に書き込みを行うのはキャッシュをフラッシュする場合だけなので、書込み頻度を減らすことができる。

問題へ

問題5

2台のプリンタがあり、それぞれの稼働率が0．7と0．6である。この2台のプリンタのいずれか一方が稼動していて、他方が故障している確率は幾らか。ここで、2台のプリンタの稼動状態は独立であり、プリンタ以外の要因は考慮しないものとする。

ア	0.18
イ	0.28
ウ	0.42
エ	0.46

解答：エ

＜解説＞

1. Aが稼働していて、Bが稼働していない確率を計算する。
   0.7×（1－0.6）＝0.7×0.4＝0.28
2. Bが稼働していて、Aが稼働していない確率を計算する。
   （1－0.7）×0.6＝0.3×0.6＝0.18
3. 1と2の加算値が2台のいずれか一方が稼動していて、他方が故障している確率である。
   0.28＋0.18＝0.46
   

したがって、エが正解である。

問題へ