平成22年度春季解答

問題1

0以上255以下の整数nに対して、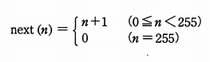



と定義する。next(n)と等しい式はどれか。ここでx AND y及びx OR yは、それぞれxとyを2進数表現にして、けたごとの論理積及び論理和をとったものとする。

ア	(n+1)AND 255
イ	(n+1)AND 256
ウ	(n+1)OR 255
エ	(n+1)OR 256

解答：ア

＜解説＞

nが0の場合、next(n)の値はn+1＝1となる。

各選択肢においてnの値を0としたとき、1となるかどうかを検証する。

以上からアのみが1となっている。

問題へ

問題2

図に示す16ビットの浮動小数点形式において、10進数0.25を正規化した表現はどれか。ここで、正規化は仮数部の最上位のけたが1になるように指数部と仮数部を調節する操作とする。

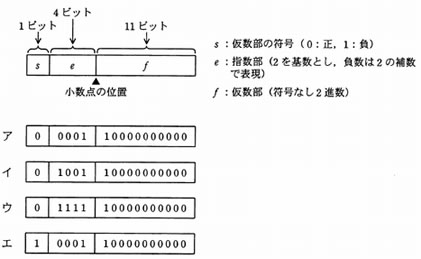
解答：ウ

＜解説＞

1. 10進数0．25を2進数で表現すると0．01になる。
2. 0．01は仮数部の最上位の桁が0になるので正規化を行う。
   
3. 0.1× 2-1 の符号(s)，指数部(e)，仮数部(f)を浮動小数点形式の各桁に当てはめる。
   1. 符号は、正なので0である。
   2. 指数部の値は-1である。負数は2の補数で表現するので、1111である。
      0001(1を2進数に変換)⇒1110(ビット列を判定)⇒1111(1を加算)
   3. 仮数部のビットは最上位桁が1になるので10000000000である。
4. したがって、が正解である。

問題へ

問題3

多数のクライアントが、LANに接続された1台のプリンタを共同利用するときの印刷要求から印刷完了までの所要時間を、待ち行列理論を適用して見積もる場合について考える。プリンタの運用方法や利用状況に関する記述のうち、M/M/1の待ち行列モデルの条件に反しないものはどれか。

ア	一部のクライアントは、プリンタの空き具合を見ながら印刷要求をする。
イ	印刷の緊急性や印刷量の多少にかかわらず、到着順に印刷する。
ウ	印刷待ち文章の総量がプリンタのバッファサイズを超えるときは、一時的に受付を中断する。
エ	一つの印刷要求から印刷完了までの所要時間は、印刷の準備に要する一定時間と印刷量に比例する時間の合計である。

解答：イ

＜解説＞

M/M/1モデルでは、次の条件が前提である。

1. 要求がランダムに発生する⇒ポアソン分布
2. 処理時間がランダムである⇒指数分布
3. 窓口は一つである
4. 優先度などの概念はなく到着順に処理される
5. 待ち行列の長さには制限はない

ア	×	1の条件に反する。
イ	○	4の条件と一致する。
ウ	×	5の条件に反する。
エ	×	4の条件に反する。

問題へ

問題4

連立一次方程式

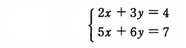
から，ｘの項の係数、ｙの項の係数、及び定数項だけを取り出した表（行列）をつくり、基本操作(1)～(3)のいずれかを順次施すことによって、解

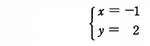
が得られた。表(行列)が次のように左から右に推移する場合、同じ種類の基本操作が施された箇所の組合せはどれか。
[基本操作]
(1) ある行に0でない数を掛ける。
(2) ある行と他の行を入れ替える。
(3) ある行に他の行の定数倍を加える。

ア	aとb
イ	aとc
ウ	bとc
エ	bとd

解答：イ

＜解説＞

操作a

1行目の2,3,4の値をすべて-2倍して2行目の5,6,7に加えている。
⇒基本操作(3)

操作b

上下の行の入れ替えである。
⇒基本操作(2)

操作c

2行目の0,3,6の値をすべて-2倍して2行目の2,3,4に加えている。
⇒基本操作(3)

操作d

2行目の0,3,6の値をすべて1/3倍することで0,1,2を得ている。
⇒基本操作(1)

したがって、(イ)aとcである。

問題へ

問題5

流れ図は、シフト演算と加算の繰り返しによって、2進整数の乗算を行う手順を表したものである。この流れ図中のa、bの組合せとして、適切なものはどれか。ここで、乗数と被乗数は符号なしの16ビットで表される。X 、Y 、Z は32ビットのレジスタであり、けた送りは論理シフトを用いる。最下位ビットを第0ビットと記す。

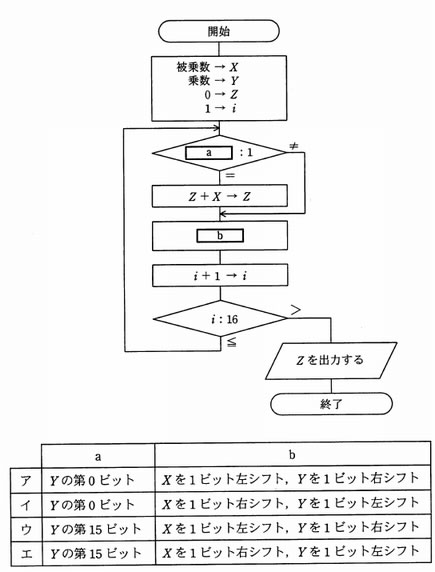
解答：ア

＜解説＞

1. 乗算はシフト演算と加算の組合せで行われる。乗算では1ビット左にシフトすると2倍になる。アまたはウが正解である。
2. 流れ図の最終出力はZである。ZはZ＋X→Zで求められている。したがって、Yの最下位ビット(0ビット)が1ならばZ＋X→Z処理を行う。アが正解である。

問題へ