平成25年度春季解答

問題1

aを正の整数とし、b=a²とする。aを2進数で表現すると、nビットであるとき、bを2進数で表現すると、高々何ビットになるか。

ア	n+1
イ	2n
ウ	n2
エ	2n

解答：イ

＜解説＞

問題分中の「高々」とは、「多くとも」の意味である。

1. a=15(おおよそ16=2⁴)とおくと15=(1111)₂となり、aは4ビットで表現できると分かる。
2. nビット居ないで表現できる2進数の数値aはおおよそ2ⁿ以内(正確には2ⁿ-1)の範囲の値となる。
3. aの2状の値は(2ⁿ)2となり、高々2nビット以内で表現できる数値となる。

したがって、イが正解である。

問題へ

問題2

解答：ア

＜解説＞

1. (A ∪B )∩(A ∪B )をド・モルガンの法則で変形する。
2. 　(A ∪B )∩(A ∪B ) = (A ∪B )∪(A ∪B ) = (A ∩B )∪(A ∩B )となる。さらに展開して変形する。
3. 　(A ∩B )∪(A ∩B ) = (A ∪A )∩(A ∪B )∩(B ∪A )∩(B ∪B ) = (A ∪B )∩(A ∪B )

となる。

したがって、アが正解である。

問題へ

問題3

図は、偶数個の1を含むビット列を受理するオートマトンの状態遷移図であり、二重丸が受理状態を表す。a,bの適切な組合せはどれか。

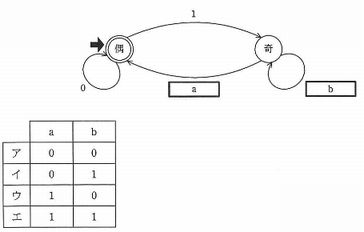
解答：ウ

＜解説＞

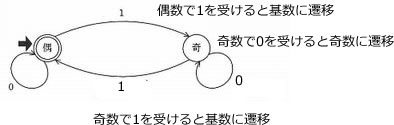
空欄aの遷移は、1の個数が奇数個から偶数個への遷移なので1である。

空欄bの遷移は、1の個数が奇数個から奇数個への遷移なので0である。

問題へ

問題4

ハミング符号とは，データに冗長ビットを付加して， 1ビットの誤りを訂正できるようにしたものである。ここでは，X₁，X₂，X₃，X₄の4ビットから成るデータに，3ビットの冗長ビットP₃，P₂，P₁を付加したハミング符号 X₁X₂X₃P₃X₄P₂P₁を考える。付加ビットP₁，P₂，P₃は，それぞれ
　 X₁⊕X₃⊕X₄⊕P₁＝0
　 X₁⊕X₂⊕X₄⊕P₂＝0
　 X₁⊕X₂⊕X₃⊕P₃＝0
となるように決める。ここで⊕は排他的論理和を表す。
　 ハミング符号 1110011 には1ビットの誤りが存在する。誤りビットを訂正したハミング符号はどれか。

ア	0110011
イ	1010011
ウ	1100011
エ	1110111

解答：ア

＜解説＞

1. X₁X₂X₃P₃X₄P₂P₁=1110011の時、問題文の各式の値がどのような値になるか計算する。

   X1⊕X3⊕X4⊕P1	＝1⊕1⊕0⊕1	0⊕1	=1
   X1⊕X2⊕X4⊕P2	＝1⊕1⊕0⊕1	0⊕1	=1
   X1⊕X2⊕X3⊕P3	＝1⊕1⊕1⊕1	0⊕1	=1

2. これらの式は本来なら全て結果が0になるように P₁～P₃が定められたはずだが結果は全部1となる。
3. したがって、これら3つの式すべてに共通して含まれているX₁のビットに誤りがあることが分かる。
4. X₁のビットを1から0に変換すると0110011となる。

したがって、アが正解である。

問題へ

問題5

探索表の構成法を例とともにa～cに示す。最も適した探索手法の組合せはどれか。ここで、探索表のコードの空欄は表の空きを示す。

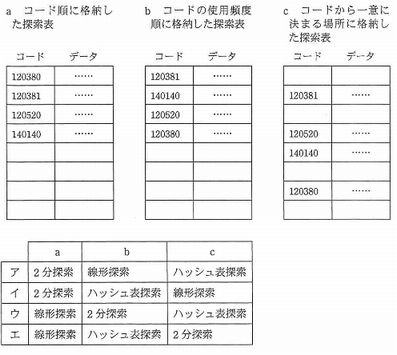
解答：ア

＜解説＞

[a コード順に格納した探索表：2分探索]

2分探索は、予めソートされたデータ列を二つに分けて、そのどちらに検索対象が含まれているか判断するという手順を再帰的に繰り返していく検索方法。
⇒aは、 コード順に格納されているので、2分探索法が適している。

[b コードの使用頻度順に格納した探索表：線形探索]

線形探索は、対象データを検索範囲のデータと先頭から順に1つずつ比較し、一致するものを検索する方法。
⇒bは、使用頻度順にならんでいるので先頭から順番に検索すると早く見つけることができるので、線形探索が適している。

[c コードから一意に決まる場所に格納した探索表：ハッシュ探索]

ハッシュ探索は、キーの値を基に格納先（記録媒体上）のアドレスを算出し、そのアドレス位置にあるデータを検索する方法。
⇒cは、コードから格納場所を探索するのでハッシュ探索が適している。

したがって、アが正解である。

問題へ