平成19年度春季解答

問題11

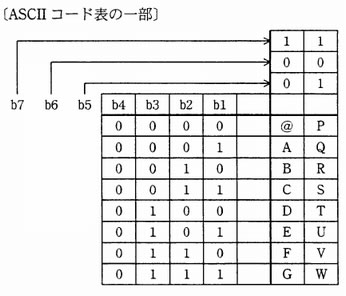
文字列“ET”を ASCII でコード化したものを 16 進表記したものはどれか。ここで，文字コードの8ビット目には，偶数パリティビットが付く。
ASCII コード表の一部〕

ア	4554
イ	A32B
ウ	ACA5
エ	C5D4

解答：エ

＜解説＞

偶数パリティではパリティビットを含め全体の1の個数が偶数となるようにパリティビットを決める。先頭の8ビット目に偶数パリティビットを付加すると文字E，TのASCIIコードは以下のようになる。

文字	ASCIIコード	パリティビットを付加	16進数に変換する
E	100 0101	1100 0101	C5
T	101 0100	1101 0100	D4

問題へ

問題12

次の2分探索木に 12 を追加したとき，追加された節 12 の位置を正しく表している図はどれか。

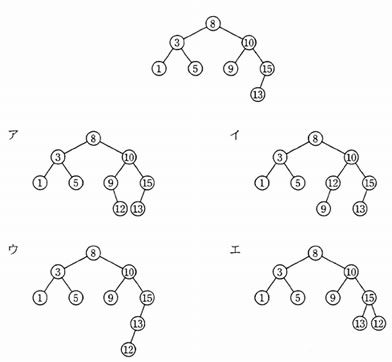
解答：ウ

＜解説＞

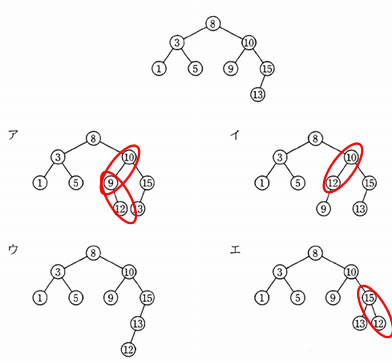
2分探索木では、「左の子の値」＜「親の値」＜「右の子の値」である必要がある。
図の赤丸で示した部分が条件にあっていない。

問題へ

問題13

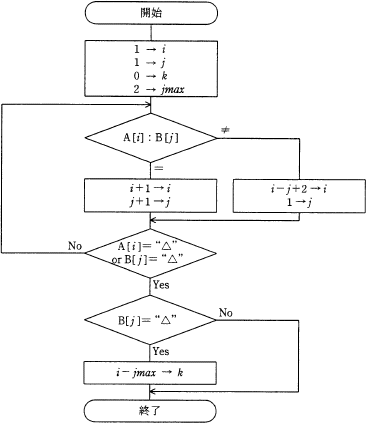
文字列 A が“aababx△”，文字列 B が“ab△”であるとき，流れ図の終了時点の k は幾らか。ここで，文字列の先頭の文字を１番目と数えるものとし，A [ i ] は A の i 番目の文字を，B [ j ] は B の j 番目の文字を，“△”は終端を示す文字を表す。

ア	0
イ	1
ウ	2
エ	4

解答：ウ

＜解説＞

1. A[1]＝“a”，B[1]＝“a”なので1回目のA[i]:B[j]の比較で文字列Aと文字列Bの先頭文字aが一致
   • i＋1→i=2
   • j＋1→j=2
2. A[2]＝“a”，B[2]＝“b”なので2回目のA[i]:B[j]の比較で文字列Aと文字列Bの2文字目が不一致
   • i－j＋2→i=2
   • 1→j→j=1
3. A[2]＝“a”，B[1]＝“a”なので3回目のA[i]:B[j]の比較で文字列Aの2文字目aと文字列Bの先頭文字aが一致
   • i＋1→i=3，
   • j＋1→j=2
4. A[3]＝“b”，B[2]＝“b”なので4回目のA[i]:B[j]の比較で文字列Aの3文字目bと文字列Bの2文字目bが一致
   • i＋1→i=4，
   • j＋1→j=3
5. ここでB[3]＝“△”となるので，判定条件A[i]＝“△”orB[j]＝“△”と，次の判定条件B[j]＝“△”の両者を満たし，i－jmax→kの処理に進む。ここでiは4，jmaxは初期値2のままなので，2→kになる。
   したがって 、kは文字列Bの先頭文字が一致した文字列Aにおける文字位置を表わしている

問題へ

問題14

配列 A[ i ]（ i ＝1，2，...， n ）を，次のアルゴリズムによって整列する。行2～3の処理が初めて終了したとき，必ず実現されている配列の状態はどれか。

	〔アルゴリズム〕
	行番号
	1	i を１から n －１まで１ずつ増やしながら行2～3を繰り返す
	2	j を n から i ＋１まで減らしながら行3を繰り返す
	3	もし A[ j ] ＜ A[ j －１] ならば，A[ j ]とA[ j －１] を交換する

ア	A[ 1 ] が最小値になる。
イ	A[ 1 ] が最大値になる。
ウ	A[ n ] が最小値になる。
エ	A[ n ] が最大値になる。

解答：ア

＜解説＞

このアルゴリズムは「バブルソート」である。
バブルソートは、隣り合う要素の大小を比較しながら整列させるソートアルゴリズムの中でも最も基本的な方法である。
ｉを1からn－1まで終了したときには、配列Ａは昇順にソートされる。

問題へ

問題15

表探索におけるハッシュ法の特徴はどれか。

ア	2分木を用いる方法の一種である。
イ	格納場所の衝突が発生しない方法である。
ウ	キーの関数値によって格納場所を決める。
エ	探索に要する時間は表全体の大きさにほぼ比例する。

解答：ウ

＜解説＞

ア	×	2分木探索に関する説明である。
イ	×	異なるキー値が同じハッシュ関数値になり衝突が発生しない方法する場合がある。
ウ	○	キーの関数値によって格納場所を決める。
エ	×	表の大きさに関係なく1回で探索できる。※衝突が発生しない場合

問題へ