必ず受かる情報処理技術者試験

当サイトは、情報処理技術者試験に合格するためのWebサイトです。
ITパスポート試験，基本情報技術者,応用情報技術者,高度試験の過去問題と解答及び詳細な解説を掲載しています。
  1. トップページ
  2. 応用情報技術者
  3. 平成23年度特別問題一覧
  4. 平成23年度特別問題2-解答・解説-分析

平成23年度特別問題

問題2

次の論理演算が成立するときに，【　a　】に入るビット列はどれか。ここで，⊕は排他的論理和を表す。

1101⊕0001⊕【　a　】⊕1101＝1111

ア 1011
イ 1100
ウ 1101
エ 1110

次の論理演算が成立するときに，【　a　】に入るビット列はどれか。ここで，⊕は排他的論理和を表す。

1101⊕0001⊕【　a　】⊕1101＝1111

ア 1011
イ 1100
ウ 1101
エ 1110

解答：エ

＜解説＞

  1. 論理積(AND)や排他的論理和(XOR)などでは交換法が成立するので、論理演算の式の順序を入れ替えても問題ない。
    計算を簡単にするために同じ値の排他的論理和(XOR)の部分を計算する。
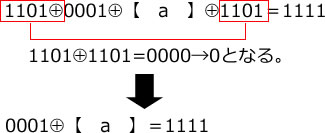
  2. 0001⊕【エ：1110】＝1111となる。

したがって、エが正解である。