平成25年度秋季解答

問題1

会員を4桁の会員番号で管理している小売店がある。 会員の中には、4と9の数字を嫌う人がいるとの理由で、会員番号は、0001、0002、0003、0005、…のように、この二つの数字を使わないように連番で発行している。 会員番号を0001から0528まで発行したとき、会員番号を付与した会員数は何人か。

ア	279
イ	344
ウ	422
エ	427

解答：ア

＜解説＞

1. 4と9以外の8つの数字で構成されることから、本問の会員番号は8進数の値とみなすことができる。
2. 一般的な8進数とは用いる数字が異なるため、それぞれを対応させると次のようになる。
   
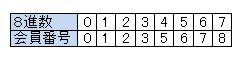
3. 対応表より最終会員番号である0528を8進数に変換すると、0427になることが分かるので、10進数に変換する
   4×8²+2×8¹+7×8⁰=256+16+7=279

問題へ

問題2

桁落ちによる誤差の説明として、適切なものはどれか。

ア	値のほぼ等しい二つの数値の差を求めたとき、有効桁数が減ることによって発生する誤差
イ	指定された有効桁数で演算結果を表すために、切捨て、切上げ、四捨五入などで下位の桁を削除することによって発生する誤差
ウ	絶対値の非常に大きな数値と小さな数値の加算や減算を行ったとき、小さい数値が計算結果に反映されないことによって発生する誤差
エ	無限級数で表される数値の計算処理を有限項で打ち切ったことによって発生する誤差

解答：ア

＜解説＞

桁落ちとは、値がほぼ等しくかつ丸め誤差を持つ数値同士の減算を行った結果、有効数字が減少することである。

ア	○	値のほぼ等しい二つの数値の差を求めたとき、有効桁数が減ることによって発生する誤差は桁落ちである
イ	×	指定された有効桁数で演算結果を表すために、切捨て、切上げ、四捨五入などで下位の桁を削除することによって発生する誤差は丸め誤差である。
ウ	×	絶対値の非常に大きな数値と小さな数値の加算や減算を行ったとき、小さい数値が計算結果に反映されないことによって発生する誤差は情報落ちである。
エ	×	無限級数で表される数値の計算処理を有限項で打ち切ったことによって発生する誤差は打切り誤差である。

問題へ

問題3

負の整数を表現する代表的な方法として、次の3種類がある。 　a 　1の補数による表現 　b 　2の補数による表現 　c 　絶対値に符号を付けた表現(左端ビットが0の場合は正、1の場合は負) 4ビットのパターン1101を a～c の方法で表現したものと解釈したとき、値が小さい順になるように三つの方法を並べたものはどれか。

ア	a、c、b
イ	b、a、c
ウ	b、c、a
エ	c、b、a

解答：エ

＜解説＞

1の補数による表現,2の補数による表現,絶対値に符号を付けた表現では、1101は次のようになる。

a：1の補数による表現

1101を1の補数による表現とすると、1101をビット反転した0010となるので、1101は10進数で－2になる。

b：2の補数による表現

1101を2の補数による表現とすると、1101をビット反転した0010に1を加算した0011となるので、1101は10進数で－3になる。

c：絶対値に符号を付けた表現

1101を絶対値に符号を付けた表現(正=0,負=1)とすると、先頭ビットは1なのでマイナスとなる。また101=5なので、1101は10進数で－5になる。

よって小さい順に並べると、-5(c)＜-4(b)＜-3(a)となる。

問題へ

問題4

論理式P、Qがいずれも真であるとき、論理式Rの真偽にかかわらず真になる式はどれか。
ここで、“￣”は否定、“∨”は論理和、“∧”は論理積、“→”は含意(“真→偽”となるときに限り偽となる演算を表す。

ア	((P→Q)∧(Q→P))→(R→Q)
イ	((P→Q)∧(Q→P))→(Q→R)
ウ	((P→Q)∨(Q→P))→(R→Q)
エ	((P→Q)∨(Q→P))→(Q→R)

解答：エ

＜解説＞

ア	×	((P→Q)∧(Q→P))→(R→Q)
イ	×	((P→Q)∧(Q→P))→(Q→R)
ウ	×	((P→Q)∨(Q→P))→(R→Q)
エ	○	((P→Q)∨(Q→P))→(Q→R)

問題へ

問題5

通信回線を使用したデータ伝送システムにM/M/1の待ち行列モデルを適用すると、平均回線待ち時間、平均伝送時間、回線利用率の関係は、次に式で表すことができる。

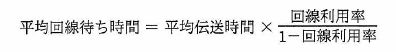
回線利用率が0%から徐々に上がっていく場合、平均回線待ち時間が平均伝送時間よりも最初に長くなるのは、回線利用率が何%を超えたときか。

ア	40
イ	50
ウ	60
エ	70

解答：イ

＜解説＞

1. 平均回転待ち時間をTw,平均伝送時間をTs,回転利用率をpとすると、
   

   Tw=	Ts×	p
   		(1－P)

   Tw/	Ts×	p
   		(1－P)

   
   となる。
2. 平均回転待ち時間が平均伝送時間よりも最初に長くなるのは、TwとTsが等しい場合なので、次のようになる。

   1=	p
   	(1－P)

   
   1-p=p
   2p=1
   p=0.5
   

問題へ