平成17年度秋季問題

問題11

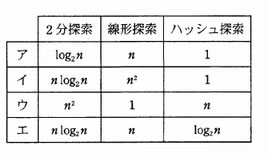
探索方法とその実行時間のオーダの正しい組合せはどれか。ここで、探索するデータ数を n とし、ハッシュ値が衝突する (同じ値になる) 確率は無視できるほど小さいものとする。また、実行時間のオーダが n² であるとは、 n 個のデータを処理する時間が cn² ( c は定数) で抑えられることをいう。

解答・解説へ

問題12

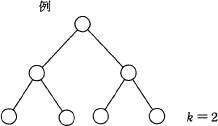
すべての葉が同じ深さをもち，葉以外のすべての節点が二つの子をもつ2分木に関して，節点数と深さの関係を表す式はどれか。ここで， n は節点数， k は根から葉までの深さを表す。例に示す2分木の深さ k は2である。

ア	n ＝ k (k＋1)＋1
イ	n ＝ 2k＋3
ウ	n ＝ 2k+1－1
エ	n ＝ (k－1)(k＋1)＋4

解答・解説へ

問題13

データ構造に関する記述のうち、適切なものはどれか。

ア	2分木は、データ間の関係を階層的に表現する木構造の一種であり、すべての節が二つの子をもつデータ構造である。
イ	スタックは、最初に格納したデータを最初に取り出す先入れ先出しのデータ構造である。
ウ	線形リストは、データ部と次のデータの格納先を指すポインタ部から構成されるデータ構造である。
エ	配列は、ポインタの付替えだけでデータの挿入・削除ができるデータ構造である。

解答・解説へ

問題14

2分探索に関する記述のうち、適切なものはどれか。

ア	2分探索するデータ列は整列されている必要がある。
イ	2分探索は線形探索より常に速く探索できる。
ウ	2分探索は探索をデータ列の先頭から開始する。
エ	n 個のデータﾌデータの探索に要する比較回数は、 n log2 n に比例する。

解答・解説へ

問題15

次の関数 f (n, k) がある。 f (4, 2) の値は幾らか。

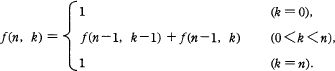
ア	3
イ	4
ウ	5
エ	6

解答・解説へ