平成17年度春季解答

問題1

次の流れ図は，10 進整数 j （0 ＜ j ＜100）を2進数に変換する処理を表している。2進数は下位けたから順に，配列の要素 NISSIN(1)から NISSIN(8) に格納される。流れ図の a 及び b に入る処理はどれか。ここで， j div 2 は j を2で割った商の整数部分を， j mod 2 は j を2で割った余りを表す。

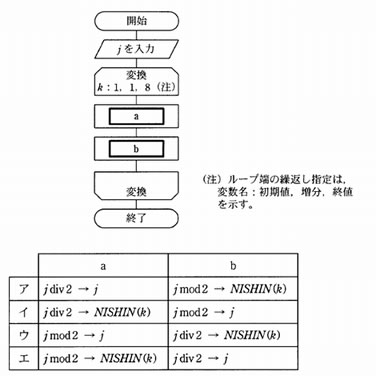
解答：エ

＜解説＞

10進数を2進数に変換するには10進数の数を2で割った剰余（余り）を求め、その商に対して除算を繰り返していく。
その過程で求められた剰余を逆に並べたものが、変換後の2進数となる。

よって正解はエである。

問題へ

問題2

ある自然数xを2進数で表現すると、1と0が交互に並んだ2nけたの2進数 1010…10 となった。このとき、xに関して成立する式はどれか。

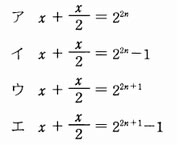
解答：イ

＜解説＞

n=2とすると、x=1010
x/2は、ｘの値を１ビット右にシフトした値なので、
x/2=0101
x ＋ x/2を計算するとすべてのビットが１になる。
よってx ＋ x/2 は2²ⁿ －1と等しくなるので正解はイである。

問題へ

問題3

負数を2の補数で表す8ビットの数値がある。この値を 10 進数で表現すると－100 である。この値を符号なしの数値として解釈すると、10 進数で幾らか。

ア	28
イ	100
ウ	156
エ	228

解答：ウ

＜解説＞

1. 10進数100を2進数8ビットで表現する。
   01100100
2. 2の補数（各値を反転させて1を足す）を求める。
   10011011
   ↓
   10011100
3. 符号なしの数値として10進数に基数変換する。
   
   

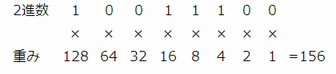
よって正解はウである。

問題へ

問題4

数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算するとよい。これは、どの誤差を抑制する方法を述べたものか。

ア	アンダフロー
イ	打切り誤差
ウ	けた落ち
エ	情報落ち

解答：エ

＜解説＞

ア	×	アンダフローとは、演算結果が、扱える数値の最小値を超えることによって生じる誤差である。演算結果が、扱える数値の最大値を超えることによって生じる誤差のことをまたオーバーフローという。
イ	×	繰り返しの計算をある条件で打ち切ることによって生じる誤差である。
ウ	×	対値がほぼ等しい数値の加減算において，上位の有効数字が失われることによって生じる誤差である。
エ	○	浮動小数点の加算において、一方の数値の下位のけたが欠落することで起きる誤差である。数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算をすることで、情報落ちの誤差を少なくすることができる。

問題へ

問題5

方程式 f (x) ＝ 0 の解の近似値を求めるアルゴリズムとして知られているニュートン法に関する記述として、適切なものはどれか。

ア	関数 f (x) が微分不可能であっても、解の近似値を求めることができる。
イ	幾何学的には、 y ＝ f (x) の接線を利用して解の近似値を求めるものである。
ウ	関数 f (x) が微分不可能であっても、解の近似値を求めることができる。
エ	どのような初期値を与えても、必ず解の近似値が得られる。

解答：イ

＜解説＞

ニュートン法は1つの初期値から求めた接線とX軸との交点から次の近似値を求め，それを元にさらに近い近似値を求めていき，許容範囲内の解を得る方法である。

問題へ