平成17年度春季問題

問題1

次の流れ図は，10 進整数 j （0 ＜ j ＜100）を2進数に変換する処理を表している。2進数は下位けたから順に，配列の要素 NISSIN(1)から NISSIN(8) に格納される。流れ図の a 及び b に入る処理はどれか。ここで， j div 2 は j を2で割った商の整数部分を， j mod 2 は j を2で割った余りを表す。

解答・解説へ

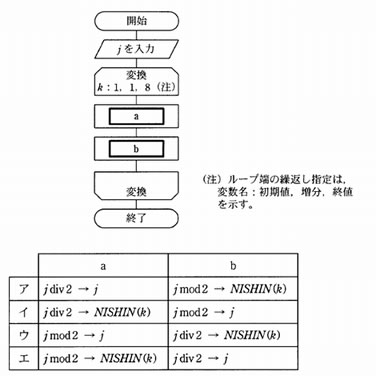
問題2

ある自然数xを2進数で表現すると、1と0が交互に並んだ2nけたの2進数 1010…10 となった。このとき、xに関して成立する式はどれか。

解答・解説へ

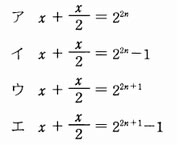
問題3

負数を2の補数で表す8ビットの数値がある。この値を 10 進数で表現すると－100 である。この値を符号なしの数値として解釈すると、10 進数で幾らか。

ア	28
イ	100
ウ	156
エ	228

解答・解説へ

問題4

数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算するとよい。これは、どの誤差を抑制する方法を述べたものか。

ア	アンダフロー
イ	打切り誤差
ウ	けた落ち
エ	情報落ち

解答・解説へ

問題5

方程式 f (x) ＝ 0 の解の近似値を求めるアルゴリズムとして知られているニュートン法に関する記述として、適切なものはどれか。

ア	関数 f (x) が微分不可能であっても、解の近似値を求めることができる。
イ	幾何学的には、 y ＝ f (x) の接線を利用して解の近似値を求めるものである。
ウ	関数 f (x) が微分不可能であっても、解の近似値を求めることができる。
エ	どのような初期値を与えても、必ず解の近似値が得られる。

解答・解説へ