- トップページ
- 基本情報技術者
- 平成17年度春季問題
- 平成17年度春季解答・解説
平成17年度春季解答
問題6
コインを4回投げたときに、表が2回だけ出る確率は幾らか。
| ア | 0.2 |
| イ | 0.375 |
| ウ | 0.5 |
| エ | 0.625 |
解答:イ
<解説>
まず、コインを 1 回投げた場合、2 通りの可能性(表か裏)がある。
よってコインを4回投げたときの起こり得る事象は 24=16 通り。
このうち表が2回だけでる組み合わせは,次の式で求めることができる。
| 4C2 | = | 4! | = | 4×3×2×1 | = | 24 | = | 6 |
| 2!(4-2)! | 2×1×2×1 | 4 |
表が2回だけ出る確率=6÷16=0.375
問題7
次の図は,ある地方の日単位の天気の移り変わりを示したものであり,数値は翌日の天気の変化の確率を表している。ある日の天気が雨のとき,2日後の天気が晴れになる確率は幾らか。
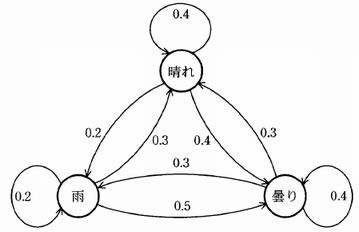
| ア | 0.15 |
| イ | 0.27 |
| ウ | 0.3 |
| エ | 0.33 |
解答:エ
<解説>
ある日の天気が雨のとき、2日後の天気が晴れになる確率を求める。
状態の移り変わり方は、以下の 3パターンがある。
- 雨 → 雨 → 晴れ
- 雨 → 曇り → 晴れ
- 雨 → 晴れ → 晴れ
それぞれのパターンがとり得る確率は、次のようになる。
| 結合度 | 確立 |
|---|---|
| 雨 → 雨 → 晴れ | 0.2 ×0.3 = 0.06 |
| 雨 → 曇り → 晴れ | 0.5 ×0.3 = 0.15 |
| 雨 → 晴れ → 晴れ | 0.3 ×0.4 = 0.12 |
したがって、雨の日の 2日後に晴れとなる確率は、
0.06 + 0.15 + 0.12 = 0.33
となる。
よって、エが正解となります。
問題8
集合 S-(T∪R) に等しいものはどれか。ここで、∩は積集合、∪は和集合、- は差集合の各演算を表す。
| ア | (S-T)- R |
| イ | (S-T) ∪ (S-R) |
| ウ | (S-T) ∪ (T-R) |
| エ | (S-T) ∩ (T-R) |
解答:ア
<解説>
ベン図より解答を求める。解説省略
問題9
8ビットのビット列の下位4ビットが変化しない操作はどれか。
| ア | 16 進表記0Fのビット列との論理積をとる。 |
| イ | 16進表記0Fのビット列との論理和をとる。 |
| ウ | 16進表記0Fのビット列との排他的論理和をとる。 |
| エ | 16進表記0Fのビット列との否定論理積をとる。 |
解答:ア
<解説>
8ビットのビット列101 0101を実際に演算する。
下位4ビットが変化しない操作はアである。

問題10
7ビットの文字コードの先頭に1ビットの偶数パリティビットを付加するとき、文字コード 30、3F、7A にパリティビットを付加したものはどれか。ここで、文字コードは 16 進数で表している。
| ア | 30、3F、7A |
| イ | 30、3F、FA |
| ウ | B0、3F、FA |
| エ | B0、BF、7A |
解答:イ
<解説>
- 文字コード 30,3F,7A を7ビットの2進数に変換する
- 30→0011 0000
- 3F→0011 1111
- 7A→0111 1010
- 先頭に1ビットの偶数パリティビットを付加します。
偶数パリティビットは,文字列内の1の数が偶数になるように先頭に0または1の値を付加します。- 0011 0000→0011 0000→30
- 0011 1111→0011 1111→3F
- 0111 1010→1111 1010→FA
お問い合わせ


