平成18年度春季解答

問題1

16 進小数 2A.4C と等しいものはどれか。

ア	25 ＋23 ＋21 ＋2－2 ＋2－5 ＋2－6
イ	25 ＋23 ＋21 ＋2－1 ＋2－4 ＋2－5
ウ	26 ＋24 ＋22 ＋2－2 ＋2－5 ＋2－6
エ	26 ＋24 ＋22 ＋2－1 ＋2－4 ＋2－5

解答：ア

＜解説＞

1. 16 進小数 2A.4C を2進数に変換する。
   
2. 2進数の桁の値と重みより変換する。
   
3. 2より2⁵ ＋2³ ＋2¹ ＋2^－2 ＋2^－5 ＋2^－6となる。

よって正解はアとなる。

問題へ

問題2

次の計算は何進法で成立するか。
131 － 45 ＝ 53

ア	6
イ	7
ウ	8
エ	9

解答：イ

＜解説＞

1の位に注目すると、7進数なのが分かる。よってイが正解である。

問題へ

問題3

負数を2の補数で表現する固定小数点表示法において、 n ビットで表現できる整数の範囲はどれか。ここで、小数点の位置は最下位ビットの右とする。

ア	－2n ～ 2n-1
イ	－2n-1 -1 ～ 2n-1
ウ	－2n-1 ～ 2n-1 -1
エ	－2n-1 ～ 2n-1

解答：ウ

＜解説＞

負数を2の補数において、nビットで表現できる整数の範囲は次のようになる。

1. 負数　－2^n-1～-1
2. 0および整数 0～ 2^n-1 -1(0を含むので最大数が1だけ小さくなる)

従って、2ⁿ個のビットパターンで－2^n-1 ～ 2^n-1 -1の範囲の整数が表現できる。

よってウが正解である。

問題へ

問題4

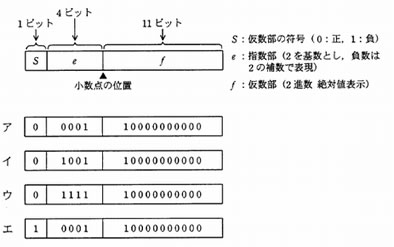
数値を図に示す 16 ビットの浮動小数点形式で表すとき，10 進数 0.25 を正規化した表現はどれか。ここでの正規化は，仮数部の最上位けたが 0 にならないように指数部と仮数部を調節する操作とする。

解答：ウ

＜解説＞

1. 10 進数 0.25 を2進数に変換する。
   
   上図より0.25₁₀＝(0.01)₂となる。
2. (0.01)₂を正規化する。
   (0.1)×2^-1 となる。
3. 浮動小数点形式で表すと次のようになる。
   

   S：	仮数部の符号	0（正）
   e：	指数部	2の補数で表現すると－1は（1111）
   f：	仮数部	10000000000（小数点以下の2進数の表示）

よってウが正解である。

問題へ

問題5

浮動小数点表示の仮数部が 23 ビットであるコンピュータで計算した場合、情報落ちが発生する計算式はどれか。ここで、( )₂内の数は2進法で表示されている。

ア	(10.101)2×2-16 － (1.001)2×2-15
イ	(10.101)2×216 － (1.001)2×216
ウ	(1.01)2×218 ＋ (1.01)2×2-5
エ	(1.001)2×220 ＋ (1.1111)2×221

解答：ウ

＜解説＞

情報落ちとは、大きな値と小さな値を加減算したときに、小さな値が無視されてしまう現象のことである。 仮数部のビット数が23ビットなので、情報落ちが発生するのは、加減算する数値の絶対値の差が2²³以上あるときです。この条件を満たすのはウだけである。よって正解はウである。

問題へ