- トップページ
- 基本情報技術者
- 平成18年度春季問題
- 平成18年度春季解答・解説
平成18年度春季解答
問題11
正三角形の内部の点から,各辺に下ろした垂線の長さの和は一定である(図1参照)。三角グラフは,この性質を利用して,三つの辺に対応させた要素の割合を各辺への垂線の長さとして表したグラフである。図2の三角グラフは,3種類のソフトについて,A~D の4人の使用率を図示したものである。正しい解釈はどれか。
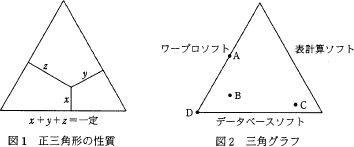
| ア | A さんは,ワープロソフトだけを使用している。 |
| イ | B さんは,ほかのソフトに比べて表計算ソフトの使用率が高い。 |
| ウ | C さんは,データベースソフト,表計算ソフト,ワープロソフトの順に使用率が高い。 |
| エ | D さんは,表計算ソフトを使用していない。 |
解答:イ
<解説>
三角グラフでは,ソフトを表す辺から離れているほどそのソフトの使用率が高くなる。
| ア | × | A さんは,ワープロソフトを使用していない。 |
| イ | ○ | B さんは,ほかのソフトに比べて表計算ソフトの使用率が高い。 |
| ウ | × | C さんは,ワープロソフト,表計算ソフト,データベースソフトの順に使用率が高い。 |
| エ | × | D さんは,表計算ソフトのみ使用している |
問題12
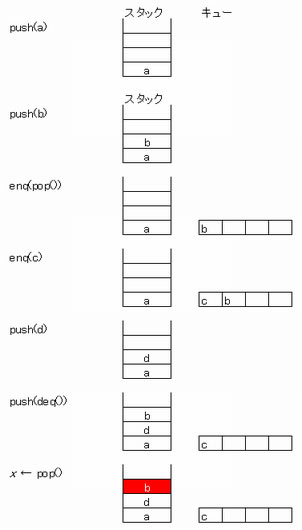
空の状態のキューとスタックの二つのデータ構造がある。次の手続を順に実行した場合、変数 x に代入されるデータはどれか。ここで、
| ア | a |
| イ | b |
| ウ | c |
| エ | d |
解答:イ
<解説>
下図より、変数xに代入されるデータはbだと分かる。よってイが正解である。
問題13
6個の数値 180,315,282,410,645,525 を並べ替える。手順1~4は途中までの手順を示したものである。手順4まで終わったときの結果はどれか。
| 手順1 | 並びの左側から順に,数値の1の位の値によって0~9のグループに分ける。 |
| 手順2 | 次に0のグループの数値を左側から順に取り出して並べ,その右側に1のグループ,以下順に2~9のグループの数値を並べていく。 |
| 手順3 | 手順2で得られた数値の並びの左側から順に,数値の 10 の位によって0~9のグループに分ける。 |
| 手順4 | 手順2と同様に,0のグループの数値から順に並べる。 |
ここで,グループ内では,処理が行われた数値を左側から順に並べるものとする。
| ア | 180,282,315,410,525,645 |
| イ | 315,410,525,180,282,645 |
| ウ | 410,315,525,645,180,282 |
| エ | 645,525,410,315,282,180 |
解答:ウ
<解説>
6個の数値 180,315,282,410,645,525を手順に従って並び替える。
| 手順1 | 並びの左側から順に,数値の1の位の値によって0~9のグループに分ける。 →
|
||||||||
| 手順2 | 次に0のグループの数値を左側から順に取り出して並べ,その右側に1のグループ,以下順に2~9のグループの数値を並べていく。 → 180,410,282,315,645,525 |
||||||||
| 手順3 | 手順2で得られた数値の並びの左側から順に,数値の 10 の位によって0~9のグループに分ける。 →
|
||||||||
| 手順4 | 手順2と同様に,0のグループの数値から順に並べる。 →410,315,525,645,180,282 |
問題14
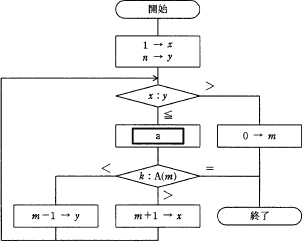
昇順に整列済の配列要素A(1),A(2),…,A(n) から,A(m)=k となる配列要素A(m) の添字 m を2分探索法によって見つける処理を図に示す。終了時点で m=0 の場合は,A(m)=k となる要素は存在しない。図中の a に入る式はどれか。ここで,/ は,小数点以下を切り捨てる除算を表す。
| ア | (x + y) → m |
| イ | (x + y)/2 → m |
| ウ | (x - y)/2 → m |
| エ | (y - x)/2 → m |
解答:イ
<解説>
2分探索法は、整列(ソート)済みのデータ列に対して行う探索方法で、データ列の中央の値を見て、検索したい値との大小関係を用いて、検索したい値が中央の値の右にあるか、左にあるかを判断して、探索範囲を狭めながら行っていく方法である。
[ a ] に入る式は,この中間点を求めて添字 m に代入する式である。
mは、中央の値になるので、( x + y ) /2 → m となる。
よってイが正解である。
問題15
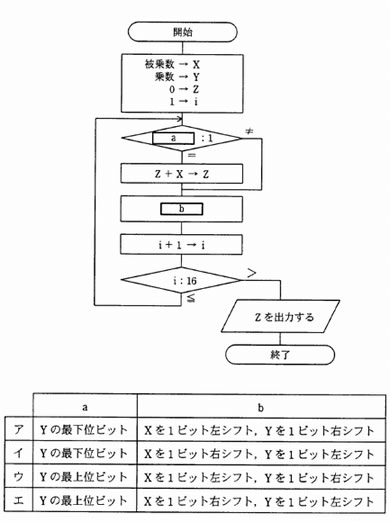
次の流れ図は,シフト演算と加算の繰返しによって2進数の乗算を行う手順を表したものである。この流れ図中の a,b の処理の組合せとして,正しいものはどれか。ここで,乗数と被乗数は符号なしの 16 ビットで表される。 X,Y,Z は 32 ビットのレジスタであり,けた送りには論理シフトを用いる。
解答:ア
<解説>
2進数の乗算は,シフト演算と加算を繰り返すことで行われる。
- 2進数は左に1ビットシフトすることで2倍の大きさになる。
- 2倍にした数に元の数を加えることで3倍の大きさにすることができる。
したがって、
| a: | 乗数の下位の1ビットの値が0の場合は,被乗数の値を左に1ビットシフトし,次の値に進む。 | |
| b: | 乗数の下位の1ビットが1の場合は,被乗数の値を足して,元の被乗数の値を左に1ビットシフトし,次の値に進む。 |
となる。よってアが正解である。
お問い合わせ


