平成19年度秋季解答

問題11

探索方法とその実行時間のオーダの正しい組合せはどれか。ここで，探索するデータ数を n とし，ハッシュ値が衝突する（同じ値になる）確率は無視できるほど小さいものとする。また，実行時間のオーダがn²であるとは，n 個のデータを処理する時間がcn²（ c は定数）で抑えられることをいう。

解答：ア

＜解説＞

2分探索

予めソートされたデータ列を二つに分けて、そのどちらに検索対象が含まれているか判断するという手順を再帰的に繰り返していく検索方法。
実行時間のオーダ＝log_２n

線形探索

対象データを検索範囲のデータと先頭から順に1つずつ比較し、一致するものを検索する方法。
実行時間のオーダ＝n

ハッシュ探索

キーの値を基に格納先（記録媒体上）のアドレスを算出し、そのアドレス位置にあるデータを検索する方法。
実行時間のオーダ＝1/dd>

よって正解は、アである

問題へ

問題12

2分木の各ノードがもつ記号を出力する再帰的なプログラムProc（ノード n ）は，次のように定義される。このプログラムを，図の2分木の根（最上位のノード）に適用したときの出力はどれか。

ア	b－c*d＋a
イ	＋a*－bcd
ウ	a＋b－c*d
エ	abc－d*＋

解答：エ

＜解説＞

1. 図の2分木の根から開始する。
2. 左の「ａ」を出力。
3. 右の「＊」に行き、さらに左の「－」に行く。
4. 左の「ｂ」を出力。
5. 右の「ｃ」を出力。
6. 上に戻り「－」を出力。
7. 「＊」の右の「ｄ」を出力。
8. 上に戻り「＊」を出力。
9. 上に戻り「＋」を出力。

したがって，abc－d＊＋が出力される。エが正解である。

問題へ

問題13

十分な大きさの配列 A と初期値が 0 の変数 p に対して，関数 f(x) と g() が次のとおり定義されている。配列 A と変数 p は，関数 f と g だけでアクセス可能である。これらの関数が操作するデータ構造はどれか。

ア	キュー
イ	スタック
ウ	ハッシュ
エ	ヒープ

解答：イ

＜解説＞

関数 f(x)

変数 p の値を１加算し、配列 A に x を格納する処理である。
この処理は変数pをスタック変数，配列要素A[p]をスタックとして，スタックにデータxの値をPUSHする処理と考えることができる。

関数 g()

配列 A から取り出した値を変数 x に格納し、変数 p の値を１減算する。
その後、変数xの値を戻り値として返す処理である。
この処理は変数pをスタック変数，配列要素A[p]をスタックとして，スタックからデータをPOPする処理と考えることができる。

よってスタックによるデータ構造であることが分かる。正解はイである。

問題へ

問題14

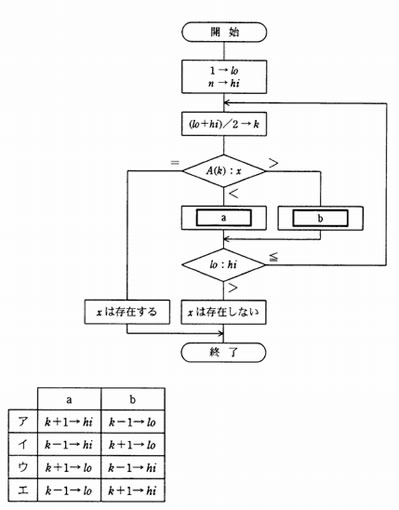
昇順に整列された n 個のデータが格納されている配列 A がある。流れ図は，2分探索法を用いて配列 A からデータ x を探し出す処理を表している。 a, b に入る操作の正しい組合せはどれか。ここで，除算の結果は小数点以下が切り捨てられる。

解答：ウ

＜解説＞

2分探索法では，探索範囲を右半分または左半分に縮小して，再びその中央のデータとの比較を繰り返すことで探索を行う。
昇順にソートされたデータ列の場合、探索範囲の中央のデータA（k ）と対象データxとを比較し、

• A（k ）＝x のときは，探索を終了する。
• A（k ）＜x であれば，対象データx は中央より右半分を探索すればよい。
  すなわち、空欄aはk ＋1→lo が適切。
• A （k ）＞x であれば対象データxは中央より左半分を探索すればよい。
  すなわち、空欄bはk －1→hi が適切。

よってウが正解である。

問題へ

問題15

整数 x, y （x ＞ y ≧ 0） に対して，次のように定義された関数 F（x, y） がある。F(231,15) の値は幾らか。ここで， x mod y は x を y で割った余りである。

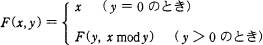
ア	2
イ	3
ウ	5
エ	7

解答：イ

＜解説＞

1. F (231, 15)	＝	F (15, 231 mod 15)
   	＝	F (15, 6)

2. F (15, 6)	＝	F (6, 15 mod 6)
   	＝	F (6, 3)

3. F (6, 3)	＝	F (3, 6 mod 3)
   	＝	F (3, 0)

問題へ