平成19年度秋季問題

問題11

探索方法とその実行時間のオーダの正しい組合せはどれか。ここで，探索するデータ数を n とし，ハッシュ値が衝突する（同じ値になる）確率は無視できるほど小さいものとする。また，実行時間のオーダがn²であるとは，n 個のデータを処理する時間がcn²（ c は定数）で抑えられることをいう。

解答・解説へ

問題12

2分木の各ノードがもつ記号を出力する再帰的なプログラムProc（ノード n ）は，次のように定義される。このプログラムを，図の2分木の根（最上位のノード）に適用したときの出力はどれか。

ア	b－c*d＋a
イ	＋a*－bcd
ウ	a＋b－c*d
エ	abc－d*＋

解答・解説へ

問題13

十分な大きさの配列 A と初期値が 0 の変数 p に対して，関数 f(x) と g() が次のとおり定義されている。配列 A と変数 p は，関数 f と g だけでアクセス可能である。これらの関数が操作するデータ構造はどれか。

ア	キュー
イ	スタック
ウ	ハッシュ
エ	ヒープ

解答・解説へ

問題14

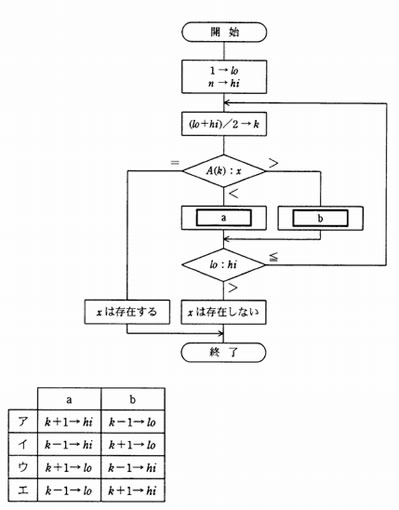
昇順に整列された n 個のデータが格納されている配列 A がある。流れ図は，2分探索法を用いて配列 A からデータ x を探し出す処理を表している。 a, b に入る操作の正しい組合せはどれか。ここで，除算の結果は小数点以下が切り捨てられる。

解答・解説へ

問題15

整数 x, y （x ＞ y ≧ 0） に対して，次のように定義された関数 F（x, y） がある。F(231,15) の値は幾らか。ここで， x mod y は x を y で割った余りである。

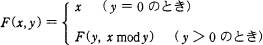
ア	2
イ	3
ウ	5
エ	7

解答・解説へ