平成23年度特別解答

問題1

論理式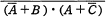と等しいものはどれか。ここで， ・は論理積，+は論理和，XはXの否定を表す。

ア	A・B+A・C
イ	A・B+A・C
ウ	(A+B)・(A+C)
エ	(A+B)・(A+C)

解答：ア

＜解説＞

ド･モルガンの法則により論理式を等価変換すると，次のようになる。

問題へ

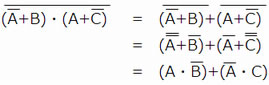
問題2

三つの実数X～Zとそれぞれの近似値が次の場合，相対誤差の小さい順に並べたものはどれか。

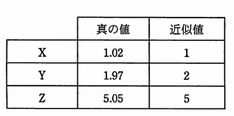
ア	X，Y，Z
イ	Y，Z，X
ウ	Z，X，Y
エ	Z，Y，X

解答：エ

＜解説＞

相対誤差は、真の値に対する絶対誤差の割合であり、次の式で求めることができる。

絶対誤差	＝	|近似値－真の値|
相対誤差	＝	（絶対誤差）÷真の値

よって

X	：	|1－1.02| ÷ 1.02 = 0.02 ÷ 1.02 ≒ 0.019
Y	：	|2－1.97| ÷ 1.97 = 0.03 ÷ 1.97 ≒ 0.015
Z	：	|5－5.05| ÷ 5.05 = 0.05 ÷ 5.05 ≒ 0.0099

となる。相対誤差の小さい順は「Z,Y,X」となる。

問題へ

問題3

表は，文字A～Eを符号化したときのピット表記と，それぞれの文字の出現確率を表したものである。1文字当たりの平均ピット数は幾らになるか。

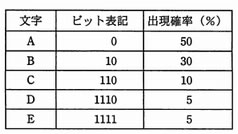
ア	1.6
イ	1.8
ウ	2.5
エ	2.8

解答：イ

＜解説＞

平均ビット数は、ビット長×出現確率の合計で計算することができる。

1. ビット長×出現確率を計算する。
   
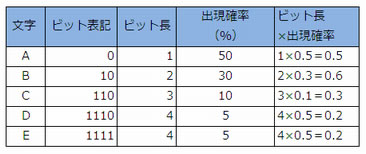
2. 合計を計算する。
   0.5＋0.6＋0.3＋0.2＋0.2＝ 1.8

問題へ

問題4

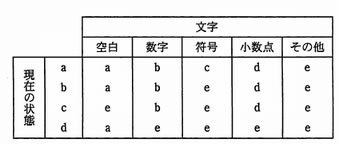
次の表は，文字列を検査するための状態遷移表である。検査では，初期状態を aとし，文字列の検査中に状態が eになれば不合格とする。
　解答群で示される文字列のうち，不合格となるものはどれか。ここで，文字列は左端から検査し，解答群中の△は空白を表す。

ア	＋0010
イ	－1
ウ	12.2
エ	9.△

解答：ウ

＜解説＞

ア	×	a(初期状態)→c(+：符号)→b(0：数字)→b(0：数字)→b(1：数字)→b(0：数字)→合格
イ	×	a(初期状態)→c(-：符号)→b(1：数字)→合格
ウ	○	a(初期状態)→b(1：数字)→b(2：数字)→d(.：小数点)→e(2：数字)→不合格
エ	×	a(初期状態)→b(9：数字)→d(.：小数点)→a(△：空白)→合格

問題へ

問題5

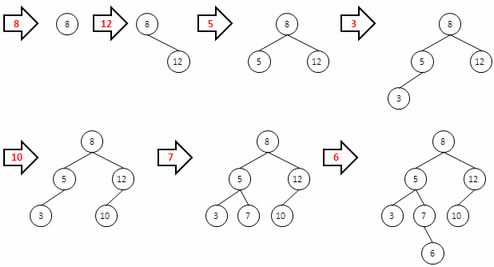
空の2分探索木に，8，12，5，3，10 7，6の順にデータを与えたときにできる2分探索木はどれか。

解答：エ

＜解説＞

問題へ