平成23年度特別解答

問題6

関数 f(x，y)が次のように定義されているとき，f(775，527)の値は幾らか。ここで，x mod yはxをyで割った余りを返す。
f(x, y): if y = 0 then return x else return f(y, x mod y)

ア	0
イ	31
ウ	248
エ	527

解答：イ

＜解説＞

1. f(775, 527)：y≠0なので、f(527, 775 mod 527) ⇒775÷527＝1余り248
2. f(527, 248)：y≠0なので、f(248, 527 mod 248)⇒527÷248＝2余り31
3. f(248, 31)：y≠0なので、f(31, 248 mod 31)⇒248÷31＝8余り0
4. f(31, 0)：y＝0なので、31を返す。

問題へ

問題7

次の流れ図は，1から100までの整数の総和を求め，結果を変数xに代入するアルゴリズムを示したものであるが，一部誤りがある。どのように訂正すればよいか。

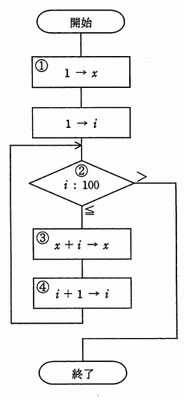
ア	①の処理を "0 → x"にする。
イ	②の条件判定を " i : 99"にする。
ウ	③の処理を "x + i → i"にする。
エ	④の処理を "x + 1→ x"にする。

解答：ア

＜解説＞

ア	○
イ	×	1から99までしか加算されない。
ウ	×	xに1から100までの総和は入らない。常に1のままである。
エ	×	繰返し処理が行われないため無限ループになる。

問題へ

問題8

整列アルゴリズムの一つであるクイックソートの記述として，適切なものはどれか。

ア	対象集合から基準となる要素を選び，これよりも大きい要素の集合と小さい要素の集合に分割する。この操作を繰り返すことで，整列を行う。
イ	対象集合から最も小さい要素を順次取り出して，整列を行う。
ウ	対象集合から要素を順次取り出し，それまでに取り出した要素の集合に順序関係を保つよう挿入して，整列を行う。
エ	隣り合う要素を比較し，逆順であれば交換して，整列を行う。

解答：ア

＜解説＞

ア	○	クイックソートに関する説明である。
イ	×	選択ソートに関する説明である。
ウ	×	挿入ソートに関する説明である。
エ	×	交換法（バブルソート）に関する説明である。

問題へ

問題9

外部割込みが発生するものはどれか。

ア	仮想記憶管理での，主記憶に存在しないページへのアクセス
イ	システムコール命令の実行
ウ	ゼロによる除算
エ	入出力動作の終了

解答：エ

＜解説＞

ア	×	内部割込みである
イ	×	内部割込みである
ウ	×	内部割込みである
エ	○	外部割込みである

問題へ

問題10

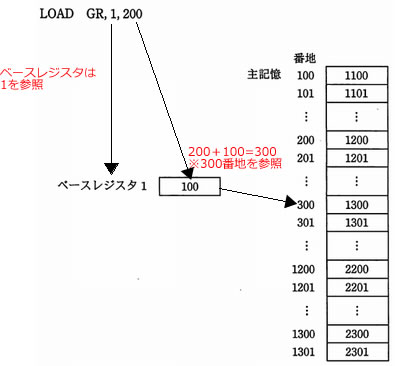
"LOAD　GR, B, AD"は，ADが示す番地にベースレジスタBの内容を加えた値を有効アドレスとして，その有効アドレスが示す主記憶に格納されているデータを汎用レジスタGRにロードする命令である。
図の状態で，次の命令を実行したとき，汎用レジスタGRにロードされるデータはどれか。

ア	1201
イ	1300
ウ	2200
エ	2300

解答：イ

＜解説＞

LOAD　GR,1,200

は、アドレス部の値（200）にベースレジスタ１の内容（100）を加えた1300 番地のアドレスに格納されているデータ（1300）を取り出す。

問題へ