平成16年度秋季解答

問題6

さいころを投げて、出た目に応じて得点するゲームを行う。出た目が 1～4 の場合はその目を得点とし、目が 5、6 の場合は得点はない。さいころを 1 回投げたときの得点の期待値は幾らか。

ア	5/3
イ	7/3
ウ	5/2
エ	20/3

解答：ア

＜解説＞

期待値とは、期待値は「平均してどのくらいの値が見込めるか」を数学的に表した数値である。

1～6の目が出る確率はそれぞれ1/6で、1～4までが得点となるので、

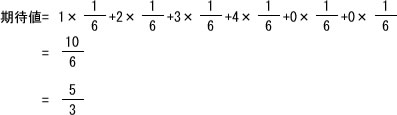
となる。よってアが正解である。

問題へ

問題7

ある工場で製造している部品の長さの誤差は，平均 0 mm，標準偏差 0.5 mm の正規分布に従っている。誤差の許容範囲が±1 mm のとき，不良品の発生率は何％になるか。標準正規分布表を用いて最も近い値を選べ。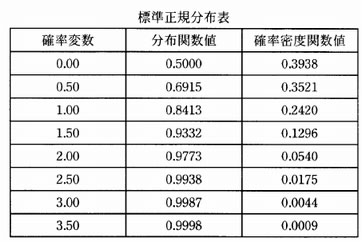

ア	2.3
イ	4.5
ウ	5.4
エ	15.9

解答：イ

＜解説＞

1. 確立変数を求める。確率変数は， （データ値－平均値）÷ 標準偏差で求めることができる。
   平均0mm，標準偏差0.5mm，データ値＋1mmの場合
   確率変数（u）＝（1－0）÷0.5＝2
2. 確率変数が2のときの分布関数値は0.9773
   これは，良品である確率なので，不良品の確率は1－0.9773 ＝ 0.0227
3. 正規分布は平均値を中心とした左右対称の分布なので，－1mmの場合も同様である。
   よって，0.0227×2＝0.0454（≒4.5％）

よってイが正解である。

問題へ

問題8

8ビットのデータの下位2ビットを変化させずに、上位6ビットのすべてを反転させる論理演算はどれか。

ア	16 進数 03 と排他的論理和をとる。
イ	16 進数 03 と論理和をとる。
ウ	16 進数 FC と排他的論理和をとる。
エ	16 進数 FC と論理和をとる。

解答：ウ

＜解説＞

8ビットの値（1010 1010）を例に計算してみる。

よってウが正解である。

問題へ

問題9

X・Y・Z ＋X・Y・Zと等価な論理式はどれか。ここで、“・”は論理積、“＋”は論理和、X は X の否定を表す。

ア	X ・ Y ・ Z
イ	X・( Y ＋ Z )
ウ	Y ・ Z
エ	Y ＋ Z

解答：ウ

＜解説＞

論理演算の分配則を使って解くことができる。

X・Y・Z+X・Y・Z	=	(X+X)・Y・Z
	=	Y・Z

問題へ

問題10

次の方法によって、データに検査数字(チェックディジット)を付加する。データにエラーが含まれていない場合、N₂＝7、N₃＝6、N₄＝2、C＝4 のとき、N₁ の値は幾らか。

　元のデータ： N₁N₂N₃N₄
　検査数字： C＝mod((N₁×1＋N₂×2＋N₃×3＋N₄×4)、10)
　　　　　　　　ここで、mod(x、10)の値は、x を 10 で割った余り
　検査数字を付加した加したデータ：N₁N₂N₃N₄C

ア	0
イ	2
ウ	4
エ	6

解答：ウ

＜解説＞

N₁N₂N₃N₄は桁の数を表し、Cはチェックディジットである。。

C ＝ mod (( N₁×1＋N₂×2＋N₃×3＋N₄×4 ) ，10 )　より

4 ＝ mod (( N₁×1＋7×2＋6×3＋2×4 ) ，10 )

4 ＝ mod (( N₁×1＋14＋18＋8) ，10 )

4 ＝ mod (( N₁＋40) ，10 )

(N1＋40)を10で割った余りが4になるようなN₁は、4になる。
よって正解はウである。

問題へ