平成24年度春季解答

問題1

次の10進小数のうち，8進数に変換したときに有限小数になるものはどれか。

ア	0.3
イ	0.4
ウ	0.5
エ	0.8

解答：ウ

＜解説＞

8進数における有限小数とは、小数部を8倍して小数部が0になる数値である。したがって、解答群それぞれを8進数に変換し、小数部が0になるものを見つければよい。

ア	×	0.3(10)→0.23146(8)…：無限小数 0.3×8＝2.4 0.4×8＝3.2 0.2×8＝1.6 0.6×8＝4.8 0.8×8＝6.4
イ	×	0.4(10) →0.31463(8)…：無限小数 0.4×8＝3.2 0.2×8＝1.6 0.6×8＝4.8 0.8×8＝6.4 0.4×8＝3.2
ウ	○	0.5(10) →0.4 (8)：有限小数 0.5×8＝4.0
エ	×	0.8(10) →0.63146(8)…：無限小数 0.8×8＝6.4 0.4×8＝3.2 0.2×8＝1.6 0.6×8＝4.8 0.8×8＝6.4

問題へ

問題2

非負の2進数 b₁b₂…b_n を3倍したものはどれか。

ア	b1b2…bn0＋b1b2…bn
イ	b1b2…bn00－１
ウ	b1b2…bn000
エ	b1b2…bn1

解答：ア

＜解説＞

2進数の各桁を左へ1桁シフトすると,

元の値が2倍になる。

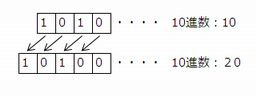
ア	○	2倍+1倍(元の値)
イ	×	4倍-1
ウ	×	8倍
エ	×	2倍+1

問題へ

問題3

隣接行列Ａで表されるグラフはどれか。ここで，隣接行列とは，ｎ個の節点から成るグラフの節点Ｖ_iとＶ_jを結ぶ枝が存在するときは第ｉ行第ｊ列と第ｊ行第ｉ列の要素が１となり，存在しないときは０となるｎ行ｎ列の行列である。

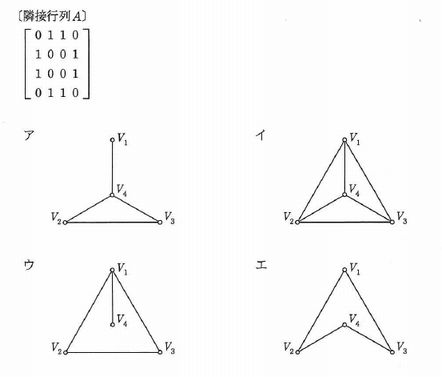
解答：エ

＜解説＞

隣接行列Aの中で1の要素だけを(i, j)の形で書き出してみます。

(1, 2) (1, 3) (2, 1) (2, 4) (3, 1) (3, 4) (4, 2) (4, 3)

このうち、例えば(1, 2)と(2, 1)はV₁とV₂を結ぶ枝が存在することを表しています。

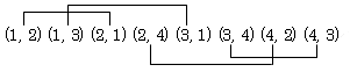
V₁とV₂、V₁とV₃、V₂とV₄、V₃とV₄が枝で結ばれた図、すなわちエが正解です。

問題へ

問題4

後置記法(逆ポーランド記法)では,例えば,式 Y=(A-B)×C を YAB-C×= と表現する。次の式を後置記法で表現したものはどれか。

Y=(A+B)×(C-D÷E)

ア	YAB+C-DE÷×=
イ	YAB+CDE÷-×=
ウ	YAB+EDC÷-×=
エ	YAB+CD-E÷×=

解答：イ

＜解説＞

逆ポーランド記法は、演算子を被演算子の後ろに配置する数式の表記法である。

逆ポーランド記法で表現すると下のようになる。

よって正解はアである。

問題へ

問題5

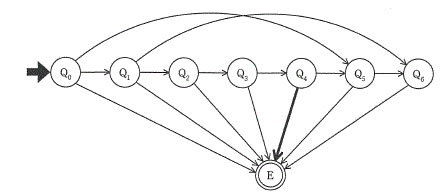
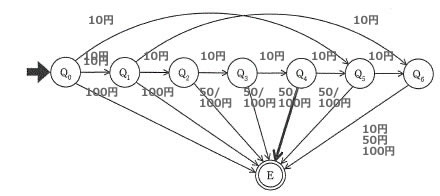
図は70円切符の自動販売機に硬貨が投入されたときの状態遷移を表している。状態Q4から状態Eへ遷移する事象はどれか。ここで,状態Q0は硬貨が投入されていない状態であり,硬貨が1枚投入されるたびに状態は矢印の方向へ遷移するものとする。 なお,状態Eは投入された硬貨の合計が70円以上になった状態であり,自動販売機は切符を発行し,釣銭が必要な場合には釣銭を返す。また,自動販売機は10円硬貨,50円硬貨,100円硬貨だけを受け付けるようになっている。

ア	10円硬貨が投入された。
イ	10円硬貨又は50円硬貨が投入された。
ウ	10円硬貨又は100円硬貨が投入された。
エ	50円硬貨又は100円硬貨が投入された。

解答：エ

＜解説＞

状態Q₁～Q₆は投入金額がまだ70円に満たない状態を表します。

それぞれの投入金額は順に0円，10円，20円，30円，40円，50円，60円になると考えられます。

状態Q₄は、投入金額が40円になった状態です。

投入金額が40円(Q₄)の状態から、投入金額が70円以上の状態(E)に遷移するには、50円または100円硬貨を投入すればよい。

問題へ