平成27年度秋季解答

問題1

0以上255以下の整数n に対して、

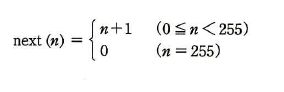
と定義する。

next(n )と等しい式はどれか。

ここで、x AND y 及びx OR y は、それぞれx とy を2進数表現にして、けたごとの論理積及び論理和をとったものとする。

ア	(n +1)AND　255
イ	(n +1)AND　256
ウ	(n +1)OR　255
エ	(n +1)OR　256

解答：ア

＜解説＞

nが0の場合、next(n)の値はn+1＝1となる。

各選択肢においてnの値を0としたとき、1となるかどうかを検証する。

以上からアのみが1となっている。

問題へ

問題2

集合A 、B 、C に対してA ∪B ∪C が空集合であるとき、包含関係として適切なものはどれか。ここで、∪は和集合を、∩は積集合を、X はX の補集合を、また、X ⊆Y はX がY の部分集合であることを表す。

ア	(A ∩B )⊆C
イ	(A ∩B )⊆C
ウ	(A ∩B )⊆C
エ	(A ∩B )⊆C

解答：エ

＜解説＞

集合A,B,Cを含むベン図は次のようになる。

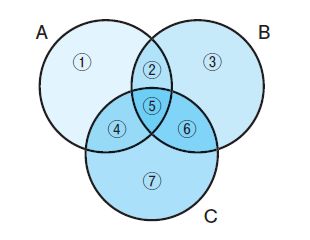
A ∪B ∪C が空集合なので、図の白色の部分(AでもBでもCでもない部分)には値がない。よってこの図でAの補集合=Aとなるのは、③,⑥,⑦の範囲である。

ア	×	(A ∩B )に該当するのは、②,⑤である。 ②はC(④,⑤,⑥,⑦)に含まれない
イ	×	(A∩B)に該当するのは、A(①,②,④,⑤)とB(①,④,⑦)の席集合である①,④である。 ①はC(④,⑤,⑥,⑦)に含まれない。
ウ	×	(A ∩B )に該当するのは、A(③,⑥,⑦)とB(②,③,⑤,⑥)の積集合である③,⑥である。 ③はC(④,⑤,⑥,⑦)に含まれない。
エ	○	(A ∩B )に該当するのは、A(③,⑥,⑦)とB(①,④,⑦)の席集合である⑦だけである。C(④,⑤,⑥,⑦)に含まれる。

問題へ

問題3

3台の機械A、B、Cが良品を製造する確率は、それぞれ60%、70%、80%である。 機械A、B、Cが製品を一つずつ製造したとき、いずれか二つの製品が良品で残り一つが不良品になる確率は何%か。

ア	22.4
イ	36.8
ウ	45.2
エ	78.8

解答：ウ

＜解説＞

1. 3台の機械A、B、Cが良品を製造する確率は、それぞれ60%=0.6、70%=0.7、80%=0.8である。
2. これらの機械が不良品を製造する確率は1-良品を製造する確率で計算できる。したがって、0.4,0.3,0.2である。
3. いずれか2つの製品が良品で残り1つが不良品になるのは次の3通りである。
   1. 機械A,Bが良品,機械Cが不良品：0.6×0.7×0.2=0.084
   2. 機械A,Cが良品,機械Bが不良品：0.6×0.3×0.8=0.144
   3. 機械B,Cが良品,機械Aが不良品：0.4×0.7×0.8=0.224
4. 発生確率の合計を計算する。
   0.084＋0.144＋0.244=0.452=45.2%

問題へ

問題4

図のように16ビットのデータを4×4の正方形状に並べ、行と列にパリティビットを付加することによって何ビットまでの誤りを訂正できるか。 ここで、図の網掛け部分はパリティビットを表す。

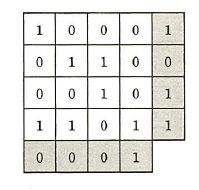
ア	1
イ	2
ウ	3
エ	4

解答：ア

＜解説＞

問題のように行と列にパリティを付加する方式は「水平垂直パリティチェック方式」という。

水平垂直パリティチェック方式では、1ビットの誤りを訂正（検出するだけでなく、元通りに直せる）できる。

したがって、アが正解である。

問題へ

問題5

キーが小文字のアルファベット1文字(a, b, …, zのいずれか)であるデータを、大きさが10のハッシュ表に格納する。 ハッシュ関数として、アルファベットのASCIIコードを10進表記法で表した時の1の位の数を用いることにする。 衝突が起こるキーの組み合わせはどれか。 ASCIIコードでは、昇順に連続した2進数が、アルファベット順にコードとして割り当てられている。

ア	aとi
イ	bとr
ウ	cとl
エ	dとx

解答：エ

＜解説＞

ハッシュ表を作成すると、次のようになる。

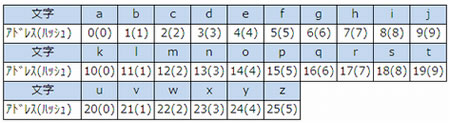
ア	×	a(0)とi(8)なので衝突しない。
イ	×	b(1)とr(7)なので衝突しない。
ウ	×	c(2)とl(1)なので衝突しない。
エ	○	d(3)とx(3)なので衝突する。

問題へ