- トップページ
- 応用情報技術者
- 平成27年度春季問題
- 平成27年度春季解答・解説
平成27年度春季解答
問題1
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し、統合後の支店にはATMを1台設置する。
統合後のATMの平均待ち時間を求める式はどれか。
ここで、待ち時間はM/M/1の待ち行列モデルに従い、平均待ち時間にはサービス時間を含まず、ATMを1台に統合しても十分に処理できるものとする。
| [条件] | |
| (1) | 平均サービス時間:Ts |
| (2) | 統合前のシステムの利用率:両支店ともρ |
| (3) | 統合後の利用者数:統合前の両支店の利用者数の合計 |
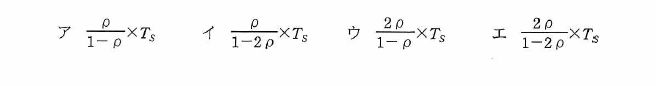
解答:エ
<解説>
- 待ち行列理論のM/M/1モデルでは窓口の平均待ち時間Twは利用率p,平均サービス時間Tsから求められる
Tw = Ts×(p/(1-p)) - 利用率pは平均到着率×平均サービス時間で求められる。統合前の客の人数をλとおくと統合前の利用率pは次のようになる。
p = λ×Ts - 統合後は一つの支店に2支店分の客がくることになるため統合後の利用率p'は次のようになる。
p' = 2λ×Ts =2p
よって、
2p × Ts 1-2p
問題2
2けたの2進数x 1x 2が表す整数をx とする。 2進数x 2x 1が表す整数を、x の式で表したものはどれか。 ここで、int(r )は非負の実数r の小数点以下を切り捨てた整数を表す。

解答:ウ
<解説>
2けたの2進数x 1x 2が表す整数をx とする。
2進数x 2x 1が表す整数を、x の式で表したものはどれか。
ここで、int(r )は非負の実数r の小数点以下を切り捨てた整数を表す。

解答:ウ
<解説>
- 2桁の2進数x 1x 2が表す整数xの値と2進数x 2x 1が表す整数yの値は次のようになる。
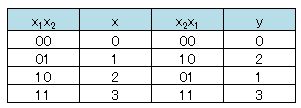
- 表からyの値はxより1だけ大きいかx以下になることが分かる。アとイの式はyの値が2倍以上になることがあるので、不適切である。
- ウとエの式の値は次のようになる。

したがって、ウが正解である。
問題3
製品100個を1ロットとして生産する。 一つのロットからサンプルを3個抽出して検査し、3個とも良品であればロット全体を合格とする。100個中に10個の不良品を含むロットが合格と判定される確率は幾らか。
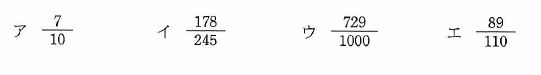
解答:イ
<解説>
- 最初の1個が良品である確率を計算する
(100-10) = 90 = 9 100 100 10 - 1個目が良品でかつ2個目も良品である確率を計算する
9 × (90-1) = 9 × 89 10 (100-1) 10 99 - 1個目,2個目が良品で3個目も良品である確率は式を約分した後に計算し、
9 × 89 × (89-1) = 9 × 89 × 88 = 178 10 99 (99-1) 10 99 98 245
となる。
したがって、イが正解である。
問題4
携帯端末に搭載されているジャイロセンサが検出できるものはどれか。
| ア | 端末に加わる加速度 |
| イ | 端末の角速度 |
| ウ | 地球上における高度 |
| エ | 地球の磁北 |
解答:イ
<解説>
ジャイロセンサは、別名角速度センサと呼ばれ、角速度を検出するデバイスである。
| ア | × | 端末に加わる加速度は、加速度センサ(Gセンサ)を用いて検出する。 |
| イ | ○ | 端末の角速度は、ジャイロセンサを用いて検出する。 |
| ウ | × | 地球上における高度は、GPSを用いて検出する。 |
| エ | × | 地球の磁北は時期センサを用いて検出する。 |
問題5
自然数をキーとするデータを、ハッシュ表を用いて管理する。 キーx のハッシュ関数h (x )を h (x ) = x mod n とすると、キーa とb が衝突する条件はどれか。 ここで、n はハッシュ表の大きさであり、x mod n はx をn で割った余りを表す。
| ア | a + b がn の倍数 |
| イ | a - b がn の倍数 |
| ウ | n がa + b の倍数 |
| エ | n がa - b の倍数 |
解答:イ
<解説>
ハッシュ値は、n=3の場合は次の表のようになる。
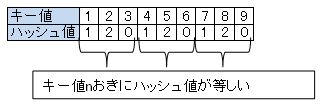
表より、二つのキー値のハッシュ値が等しくなる条件はキー値の差(a-b)がnの倍数であるときということが分かる。
お問い合わせ


