平成18年度秋季解答

問題1

1バイトのデータで0のビット数と1のビット数が等しいもののうち、符号なしの2進整数として見たときに最大になるものを、10進整数として表したものはどれか。

ア	120
イ	127
ウ	170
エ	240

解答：エ

＜解説＞

1. 1バイトのデータを「符号なしの２進整数として見たときに最大になるもの」は、 1111 1111 である。
   設問では、「1バイトのデータで0のビット数と1のビット数が等しいもの」との記述があるので、1と0がそれぞれ4つずつ現れるようにすればよい。
   2進数でも左側に行くほど重み付けが大きくなるので、最大数は1111 0000になる。
2. (1111 0000)₂を10進数に変換する。
   

   (11110000)2	＝	1×27＋1×26＋1×25＋1×24＋0×23＋0×22＋0×21＋0×20
   	＝	128＋64＋32＋16＋0＋0＋0＋0
   	＝	240

よってエが正解である。

問題へ

問題2

数値を2進数で格納するレジスタがある。このレジスタに正の整数xを設定した後、”レジスタの値を2ビット左にシフトして、xを加える”操作を行うと、レジスタの値はxの何倍になるか。ここで、シフトによるあふれ (オーバーフロー) は、発生しないものとする。

ア	3
イ	4
ウ	5
エ	6

解答：ウ

＜解説＞

1 ビット左シフトするごとに 2 倍になるので，x を 2 ビット左シフトしたものに x を加えると，x×2×2＋x＝5x→ 5 倍になる。よってウが正解である。

下記より、(3)₁₀から(15)₁₀になる（5倍）ことが分かる。

1. レジスタの値を2ビット左にシフトする。
   

   (11)2	→	(1100)2
   (3)10	→	(12)10

2. xを加える
   

   (12)10+(3)10

   =

   (15)10

問題へ

問題3

8ビットで表される符号なし2進数xが16の倍数であるかどうかを調べる方法として、適切なものはどれか。

ア	xと2進数00001111のビットごとの論理積をとった結果が0である。
イ	xと2進数00001111のビットごとの論理和をとった結果が0である。
ウ	xと2進数11110000のビットごとの論理積をとった結果が0である。
エ	xと2進数11110000のビットごとの論理和をとった結果が0である。

解答：ア

＜解説＞

1. 16(10000)₂の倍数=16(10000)₂で割ったあまりが0である。すなわち、1(0001)₂～15(1111)₂の値が存在しなければ16の倍数になる。

   (1)10	：	(0001)2
   (15)10	：	(1111)2
   (16)10	：	(10000)2

2. 1より下位4ビットが全て0ならば16の倍数であることが分かる。
3. 下位4ビットを取り出し、それが0かどうかを調べるのは、x と２進数 00001111 のビットごとの論理積をとることである。

問題へ

問題4

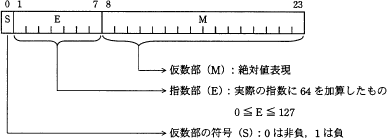
次の 24 ビットの浮動小数点形式で表現できる最大値を表すビット列を， 16 進数として表したものはどれか。ここで，この形式で表現される値は (－1)^S ×16^E－64×0.M である。

ア	3FFFFF
イ	7FFFFF
ウ	BFFFFF
エ	FFFFFF

解答：イ

＜解説＞

1. 24 ビット浮動小数点形式で正の最大値は次の内容になる。

   仮数部の符号が正	0
   指数部が正の最大値	111 1111
   仮数部の絶対値が最大	1111 1111 1111 1111

   
2. 0111 1111 1111 1111 1111 1111を16進数に変換する。
   

よって正解はエである。

問題へ

問題5

負数を2の補数で表す16ビットの符号付き固定小数点数の最小値を表すビット列を、16進数として表したものはどれか。

ア	7FFF
イ	8000
ウ	8001
エ	FFFF

解答：イ

＜解説＞

2進数を2の補数で表す場合の範囲は、-2^n-1-1 ～ 2^n-1となります。

最大値	-215-1	＝	32,767	＝	7FFF16
最小値	215	＝	-32,768	＝	800016

よって正解はイである。

問題へ