平成18年度秋季解答

問題6

浮動小数点形式で表現される数値の演算において、有効けた数が大きく減少するものはどれか。

ア	絶対値がほぼ等しく、同符号である数値の加算
イ	絶対値がほぼ等しく、同符号である数値の減算
ウ	絶対値の大きな数と絶対値の小さな数の加算
エ	絶対値の大きな数と絶対値の小さな数の減算

解答：イ

＜解説＞

絶対値がほぼ等しく，同符号である数値の減算では，その差がわずかであるために有効けた数が減少する。
有効けた数が減少することによって生ずる誤差のことをけた落ちという。

ア	×	有効桁数はほとんど変わらない。
イ	○	有効けた数が大きく減少する。
ウ	×	情報落ちの誤差が発生する可能性がある。
エ	×	情報落ちの誤差が発生する可能性がある。

問題へ

問題7

男子3人、女子5人の中から3人を選ぶとき、男子が少なくとも1人含まれる選び方は何通りあるか。

ア	21
イ	30
ウ	46
エ	56

解答：ウ

＜解説＞

男子が少なくとも1人含まれる選び方は、 「全部の組み合わせ－３人とも女子の場合」 である。

全部の組み合わせ	＝	8C3	＝	8×7×6	＝	56
				3×2×1

３人とも女子の場合	＝	5C3	＝	5×4×3	＝	10
				3×2×1

男子が少なくとも1人含まれる選び方

＝

56-10

＝

46

よって正解はウである。

問題へ

問題8

次に示す手順は、列中の少なくとも一つは1であるビット列が与えられたとき、最も右にある1を残し、ほかのビットをすべて0にするアルゴリズムである。例えば、00101000が与えられたとき、00001000が求まる。aに入る論理演算はどれか。

手順1	与えられたビット列 A を符号なしの２進数と見なし，A から１を引き，結果を B とする。
手順2	A と B の排他的論理和（ XOR ）を求め，結果を C とする。
手順3	A と C の【　a　】 を求め，結果を A とする。

ア	排他的論理和 (XOR)
イ	否定論理積 (NAND)
ウ	論理積 (AND)
エ	論理和 (OR)

解答：ウ

＜解説＞

ビット列Ａが、00101000 を例に説明する。

手順3で(a)を求めて結果が00001000となるのは、ウ）論理積 (AND)である。

問題へ

問題9

次の真理値表で，変数 X ，Y ，Z に対する関数 F を表す式はどれか。ここで，“・”は論理積，“＋”は論理和，Aは A の否定を表す。

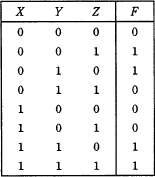
ア	X・Y＋Y・Z
イ	X・Y・Z＋Y
ウ	X・Y・Z＋X・Y＋Y・Z
エ	X・Y・Z＋X・Y＋Y・Z

解答：ウ

＜解説＞

それぞれの関数式に X, Y, Z の各値を入れる。

X＝0、Y＝0、Z＝0 を代入する。

ア	○	X・Y＋Y・Z	＝	0・0＋0・1＝0
イ	○	X・Y・Z＋Y	＝	0・0・1＋0＝0
ウ	○	X・Y・Z＋X・Y＋Y・Z	＝	1・1・0＋0・0＋0・1＝0
エ	×	X・Y・Z＋X・Y＋Y・Z	＝	1・1・0＋0・1＋1・1＝1

X＝0、Y＝0、Z＝1 を代入する。

ア	×	X・Y＋Y・Z	＝	0・0＋0・0＝0
イ	×	X・Y・Z＋Y	＝	0・0・0＋0＝0
ウ	○	X・Y・Z＋X・Y＋Y・Z	＝	1・1・1＋0・0＋0・0＝1

よってウが正解である。

問題へ

問題10

長さ3の文字列c₁c₂c₃の中には、長さ2以上の連続した部分文字列としてc₁c₂、c₂c₃、c₁c₂c₃の三つがある。長さ100の文字列c₁c₂・・・c1₀₀の中に、長さ10以上の連続した部分文字列が全部で幾つあるかを求める式はどれか。

ア	1＋2＋3＋・・・・＋88＋89
イ	1＋2＋3＋・・・・＋89＋90
ウ	1＋2＋3＋・・・・＋90＋91
エ	1＋2＋3＋・・・・＋98＋99

解答：ウ

＜解説＞

(1)	長さ 100 の文字列の中に長さ 100 の連続した部分文字列は、1個
(2)	長さ 100 の文字列の中に長さ 99 の連続した部分文字列は、2個
(3)	長さ 100 の文字列の中に長さ 98 の連続した部分文字列は、3個
(4)	長さ 100 の文字列の中に長さ 97 の連続した部分文字列は、4個
	：
(91)	長さ 100 の文字列の中に長さ 10 の連続した部分文字列は、91 個

となる。よってウが正解である。

問題へ